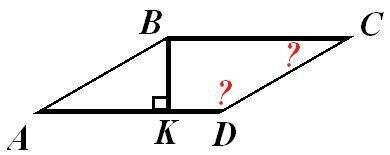
Чертеж - во вложении.
Т.к. ВК⊥AD, то Δ АВК - прямоугольный, в котором по условию гипотенуза АВ в 2 раза больше катета ВК (BK=AB:2). Значит, в этом треугольнике против катета ВК лежит ∠А = 30°.
По свойству противоположных углов параллелограмма ∠С=∠А=30°.
По свойству углов параллелограмма, прилежащих к одной стороне, ∠С+∠D=180° ⇒ ∠D = 180°-30°=150°.
Ответ: ∠С=30°, ∠D=150°.