1) Во-первых, треугольник в котором две биссектрисы равны является равнобедренным. Отсюда сразу напишем ответ: p=9+9+6 = 24 см;
Теперь докажем утверждение
1)
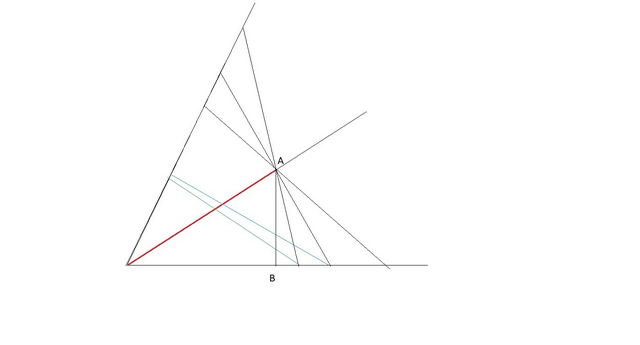
Возьмем угол и проведем в нем биссектрису данной длины. Пусть длина равна l. Теперь будем выбирать точки на луче (назовем его луч 1) данного угла и через конец биссектрисы проводить множество прямых. Они будут пересекаться со вторым лучом угла и будут образовывать угол с ним. Рассмотрим множество получившихся углов. Из каждой вершины угла проведем ее биссектрису до пересечения с лучом 1. Исключим из рассмотрения все биссектрисы длины которых не равны l; Итак, перед нами множество биссектрис с длинами l; Докажем, что любые две могут образовать треугольник. Рассмотрим две крайние биссектрисы. Расстояние между ними

, где x - расстояние AB (см. рис.); Это первая сторона треугольника. Две другие равны l; Очевидно, что

; Поэтому с любые две биссектрисы образуют треугольник. С другой стороны, в равнобедренном тупоугольном треугольнике не могут быть равны основание и сторона. Значит множество рассматриваемых биссектрис может содержать лишь одну биссектрису длины l; Другими словами, существует лишь один треугольник с двумя равными биссектрисами данной длины и с данным единственным углом. Но для таких параметров легко подобрать равнобедренный треугольник, в котором очевидно равны биссектрисы, выходящие из равных углов. Значит найденный нами единственный треугольник - равнобедренный, что и доказывает утверждение
(1);
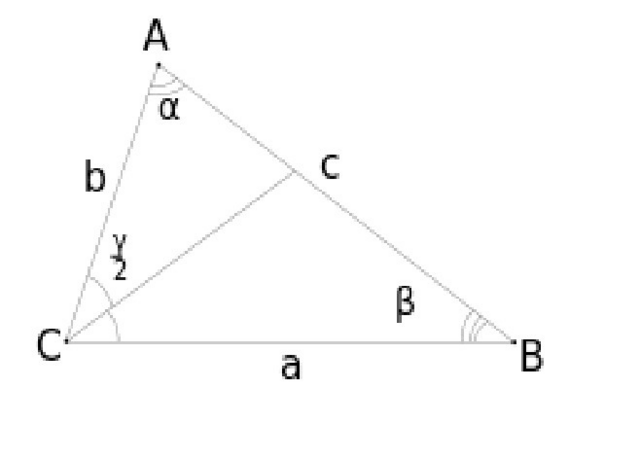
Доказать можно было проще: формула биссектрисы -

; Другой биссектрисы:

; Поскольку l=l', то