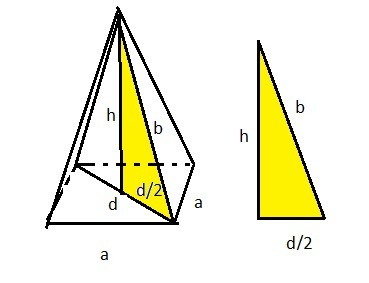
Для нахожднения объема надо найти высоту пирамиды
a=6√2
b=10
высота h
диагональ основания d
по теореме Пифагора
d²=a²+a²=2a²=2(6√2)²=2*36*2=144
d=√144=12
половина диагонали d/2=12/2=6
половина диагонали, боковое ребро и высота образуют прямоугольный треугольник в котором боковое ребро является гипотенузой а высота и половина диагонали являются катетами
по теореме Пифагора
b²=h²+(d/2)²
h²=b²-(d/2)²=10²-6²=100-36=64
h=√64=8
V=(1/3)Sоснования*h=(1/3)(6√2)²*8=(1/3)72*8=24*8=192 см³