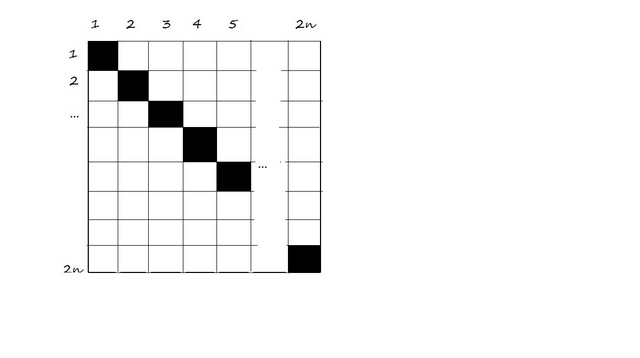
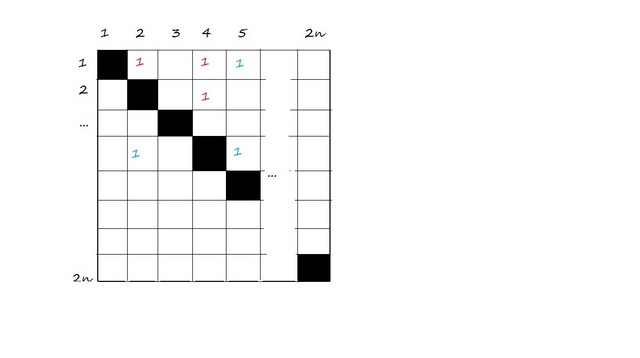
Построим таблицу 2n×2n (см. рис). Столбцы и строки обозначают вершины (они занумерованы числами от 1 до 2n). Если какие-то вершины соединены ребром, то на соответствующем пересечении столбца и строки напишем 1. Например, если вершины 4 и 2 соединены ребром, то на пересечении 4 столбца и 2 строки напишем 1. Поскольку 4 столбец и четвертая строка отвечают за одну и ту же вершину, можем обрезать таблицу пополам (по линии диагонали). Заметим, если три вершины образуют треугольник, то единицы, соответствующие этим соединениям образуют прямоугольный треугольник (если мысленно их соединить в таблице). Также, любой двойке единиц в конкретном столбце соответствует единственная единица в соответствующей строке, такая что они втроем образуют треугольник. Например, на рисунке красные единицы образуют треугольные, а синие - нет. При этом двойке красных единиц в 4-ом столбце соответствует единственная 1-ца, такая, что они вместе образуют треугольник (если бы третья единица была в 3-ем столбце, 1 строке, то треугольник не образовывался). Значит общее число треугольников в графе соответствует сумме комбинаций двоек в каждом столбце. Пусть в первом столбце n₁ единиц, во втором n₂ и т.д. Значит общее число треугольников равно  (*); Заметим, что минимальное значение выражения A²-A для натуральных чисел равно 1. Раз
(*); Заметим, что минимальное значение выражения A²-A для натуральных чисел равно 1. Раз  , то с учетом (*), минимальное количество треугольников равно 2n/2 = n; То есть ясно, что хотя бы один треугольник образуется
, то с учетом (*), минимальное количество треугольников равно 2n/2 = n; То есть ясно, что хотя бы один треугольник образуется