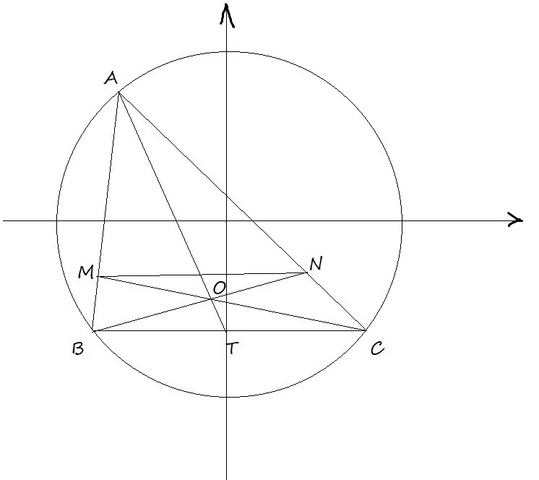
Поскольку  , то треугольники MAN и BAC подобны. Значит MN параллелен BC ⇔ BMNC - трапеция. При этом BN и MC - диагонали. В трапеции отрезок, соединяющий середины оснований, продолжения боковых сторон и точка пересечения диагоналей лежат на одной прямой. Следовательно, AT - медиана треугольника ABC. Заметим, что отношение "расстояний" пройденных точками A и O равно искомому отношению диаметров окружностей, что равно отношению радиусов. Точка T зафиксирована. Спроецируем путь пройденный точкой O на вертикальную ось. Получим длину диаметра окружности. Данный диаметр пропорционален длине отрезка OT. Точка A пройдет весь путь окружности, проекция этого пути равна диаметру описанной окружности. Так как точка O лежит на отрезке AT, то пройденный путь пропорционален диаметру описанной окружности с тем же коэффициентом пропорциональности, что и отношение отрезка OT к соответствующему пути. Получили, что искомое отношение радиусов равно отношению
, то треугольники MAN и BAC подобны. Значит MN параллелен BC ⇔ BMNC - трапеция. При этом BN и MC - диагонали. В трапеции отрезок, соединяющий середины оснований, продолжения боковых сторон и точка пересечения диагоналей лежат на одной прямой. Следовательно, AT - медиана треугольника ABC. Заметим, что отношение "расстояний" пройденных точками A и O равно искомому отношению диаметров окружностей, что равно отношению радиусов. Точка T зафиксирована. Спроецируем путь пройденный точкой O на вертикальную ось. Получим длину диаметра окружности. Данный диаметр пропорционален длине отрезка OT. Точка A пройдет весь путь окружности, проекция этого пути равна диаметру описанной окружности. Так как точка O лежит на отрезке AT, то пройденный путь пропорционален диаметру описанной окружности с тем же коэффициентом пропорциональности, что и отношение отрезка OT к соответствующему пути. Получили, что искомое отношение радиусов равно отношению  . Пусть MB = x, AM = 3x; AN = 3y; NC = y; TC = BT; По теореме Менелая:
. Пусть MB = x, AM = 3x; AN = 3y; NC = y; TC = BT; По теореме Менелая:  , Значит
, Значит  ; Ответ: 7:1
; Ответ: 7:1