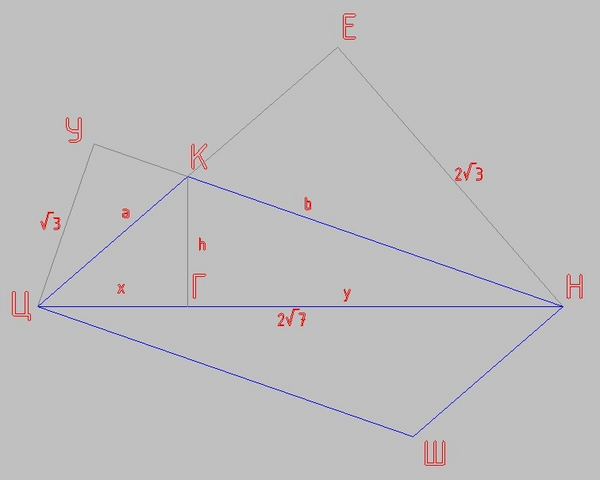
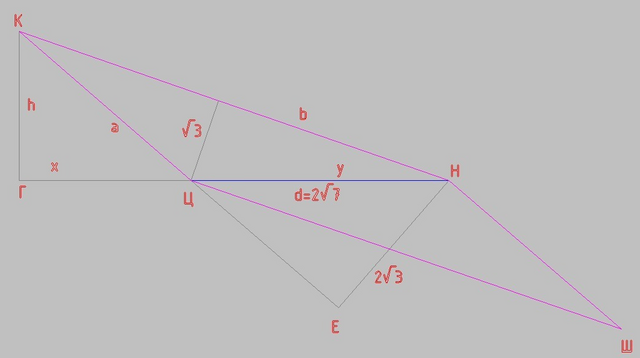
Диагональ параллелограмма ЦН высотой КГ делится на отрезки ЦГ и ГН
x+y = 2√7
Теорема Пифагора для ΔЦКГ
a² = x² + h²
Теорема Пифагора для ΔНКГ
b² = y² + h²
ΔЕНЦ и ΔКГН подобны - один угол общий, второй угол прямой
2√7/√3 = b/h
ΔЦУН и ΔКГН подобны - один угол общий, второй угол прямой
2√7/(2√3) = a/h
-----------
Пять переменных, пять уравнений. Можно начинать, всё готово.
a = h√7/√3
b = h(2√7)/√3
подставляем в три другие уравнения
---
x + y = 2√7
h²7/3 = x² + h²
h²4*7/3 = y² + h²
---
x + y = 2√7
h²4/3 = x²
h²25/3 = y²
---
полагаем, x>0 y>0
x + y = 2√7
h*2/√3 = x
h*5/√3 = y
---
h*2/√3 + h*5/√3 = 2√7
7h/√3 = 2√7
h₁ = 2√3/√7
a₁ = h₁√7/√3 = 2
b₁ = h₁(2√7)/√3 = 4
S₁ = 2√7*h₁ = 4√3
S₁² = 16*3 = 48
---
Попробуем ещё варианты, при которых высота ГК находится на продолжении диагонали ЦН
полагаем, x<0 y>0
x + y = 2√7
h*2/√3 = -x
h*5/√3 = y
---
-h*2/√3 + h*5/√3 = 2√7
3h/√3 = 2√7
h√3 = 2√7
h₂ = 2√7/√3
a₂ = h₂√7/√3 = 14/3
b₂ = h₂(2√7)/√3 = 28/3
S₂ = 2√7*h₂ = 28/√3
S₂² = 784/3
---
Ещё вариант, попробуем передвинуть высоту в другую сторону, если получится
полагаем, x>0 y<0</p>
x + y = 2√7
h*2/√3 = x
h*5/√3 = -y
---
h*2/√3 - h*5/√3 = 2√7
-3h/√3 = 2√7
-h√3 = 2√7
h = -2√7/√3
Нет, третьего решения нет.
Как нет и четвёртого решения с x<0 y<0</p>
Итак, ответ
S₁² = 48
S₂² = 784/3