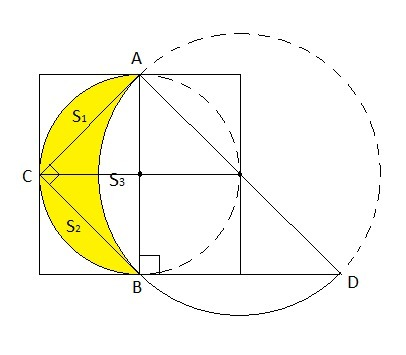
Треугольники ABD и ABC – прямоугольные и равносторонние, AB = BD, AC = BC.
AB – катет △ABD, гипотенуза △ ABC и диаметр меньшего полукруга, AD – гипотенуза △ABD и диаметр большего полукруга.
Теорема Евклида о прямоугольном треугольнике (обобщение теоремы Пифагора):
Если на катетах и гипотенузе прямоугольного треугольника построить какие-либо подобные фигуры a, b, c, у которых катеты и гипотенуза данного треугольника являются соответствующими сторонами, то Sa + Sb = Sc, где Sa, Sb и Sc – площади подобных фигур.
С учётом вышесказанного, так как сегмент S3 отсекается от большего полукруга катетом △ABD, а сегменты S1 и S2 от меньшего полукруга катетами △ABC. Значит, сегмент S3 подобен сегментам S1 и S2, а сумма площадей S1 и S2 равна площади S3. Следовательно, площадь закрашенной области равна площади треугольника ABC, и если площадь одной клетки равна 1 ед², то и площадь треугольника ABC также равна 1 ед².