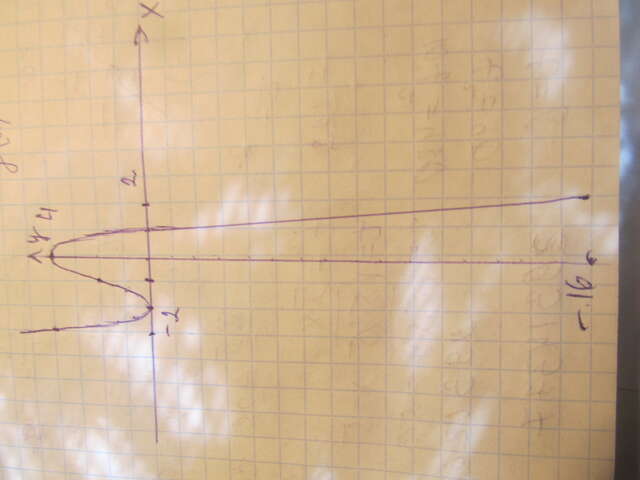
F(x)=-x^3-3x^2+4;
F'(x)=-3x^2-6x;
3x^2+6x=0;
3x(x+2)=0;
x1=0; x2=-2. x2∉[-1;2]
F(x) I [-1;0) I 0 I (0;2]
--------------------------------------
F'(x) I + I 0 I -
----------------------------------------
F(x) I возр. I max I убыв. Fmax=4 при х=0 (точка максимума)
Найдем значения на концах промежутка
F(-1)=2 ⇒ наибольшее значение ф-ции на промежутке [-1;2] F(0)=4.
F(2)=-16 - наименьшее значение ф-ции на этом промежутке.
F(x) возрастает при х∈[-1;0], убывает при х∈[0;2].