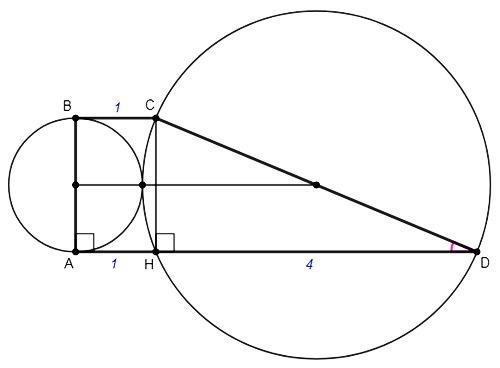
Точка касания двух окружностей лежит на линии их центров. Поскольку центрами являются середины боковых сторон, линией центров является средняя линия трапеции и она равна сумме радиусов или полусумме боковых сторон. А так как средняя линия трапеции равна полусумме оснований, сумма боковых сторон равна сумме оснований.
BC=x, AD=5x
AB+CD=AD+BC=6x
CH - высота, CH=AB
HD=AD-BC=4x
CH+CD=6x <=> CH=6x-CD
CH^2 + HD^2 = CD^2 <=>
(6x-CD)^2 + (4x)^2 = CD^2 <=>
36x^2 -12xCD +CD^2 +16x^2 = CD^2 <=>
CD= 52/12 *x =13/3 *x
cos(D) =HD/CD =4*3/13 =12/13
∠D= arccos(12/13) =22,62°