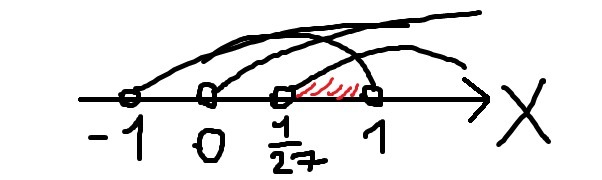
0 \\ \dfrac{1}{x}+1>0 \\ 27x - 1 > 0 \\ x \ne 0 \end{gathered} \right.$ \ \ \ \ ; \ \ \ $\left\{ \begin{gathered} x > 0 \\ x < 1 \\ x > \dfrac{1}{27} \\ x > -1 \end{gathered} \right.$ \ (1) " alt=" \log _{2}(\dfrac{1}{x} -1) + \log _{2} ( \dfrac{1}{x} + 1) \le \log _{2}(27x-1) \\ \\ ODZ: \ $\left\{ \begin{gathered} \dfrac{1}{x} -1 > 0 \\ \dfrac{1}{x}+1>0 \\ 27x - 1 > 0 \\ x \ne 0 \end{gathered} \right.$ \ \ \ \ ; \ \ \ $\left\{ \begin{gathered} x > 0 \\ x < 1 \\ x > \dfrac{1}{27} \\ x > -1 \end{gathered} \right.$ \ (1) " align="absmiddle" class="latex-formula">
0 \\ \\ 1 - 27x^{3} \le 0 \\ \\ 27x^{3} \ge 1 \\ \\ x \ge \dfrac{1}{3} " alt=" \log _{2}(\dfrac{1}{x} -1) + \log _{2} ( \dfrac{1}{x} + 1) \le \log _{2}(27x-1) \\ \\ \log _{2}((\dfrac{1}{x} -1)(\dfrac{1}{x} + 1)) \le \log _{2}(27x -1) \\ \\ \log _{2}(\dfrac{1}{x^{2}} -1) \le \log _{2}(27x-1) \\ \\ \dfrac{1}{x^{2}} - 1 \le 27x -1 \\ \\ \dfrac{1}{x^{2}} - 1 - 27x +1 \ \le 0 \\ \\ \dfrac{1}{x^{2}} - 27x \le 0 \\ \\ \dfrac{1-27x^{3}}{x^{2}} \le 0 \ / * x^{2}, T.K. \ x^{2} > 0 \\ \\ 1 - 27x^{3} \le 0 \\ \\ 27x^{3} \ge 1 \\ \\ x \ge \dfrac{1}{3} " align="absmiddle" class="latex-formula">
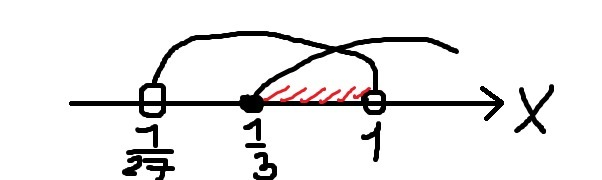
С учётом ОДЗ (2):
Ответ: x ∈ [1/3 ; 1)
