Докажите, что отрезок соединяющий середины противоположных сторон выпуклого...

Question

Докажите, что отрезок соединяющий середины противоположных сторон выпуклого четырехугольника меньше полусуммы его диагоналей
7 класс

Answer 1

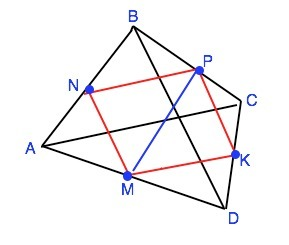
Пусть дан выпуклый четырехугольник АВСD. Точки K, M, N, P, - последовательно середины его сторон (K∈СD).

В ∆ BCD отрезок РК соединяет середины ВС и СD, является седней линией и потому равен половине диагонали BD,

Аналогично отрезок МК - средняя линия ∆ АСD и равен половине диагонали АС.

РК+МК=(АС+ВD):2 - полусумма диагоналей.

В ∆ МРК сторона МР меньше суммы сторон РК и МК ( неравество треугольника), ч.т.д.

---