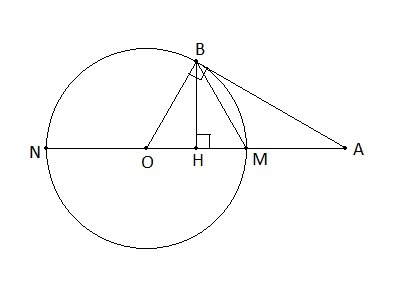
1) Для касательной и секущей к окружности, проведённых из одной точки, квадрат расстояния от этой точки до точки касания равен произведению длины секущей на длину её внешней части.
Значит, AB²= AN * AM; AN = AB²/ AM; AN = (√3)²/1 = 3; MN – диаметр;
OB = OM = ON = R = (AN – AM)/2; R = (3 – 1)/2 = 1; AO = AM + OM; AO = 1+1 = 2.
2) △OBA – прямоугольный; BH – высота; ⟹ △OBH ≈ △OBA; △OBH ≈ △HBA.
Значит, OH/OB = OB/OA; OH = OB²/OA; OH = 1²/2 = 0,5; AH = OA – OH;
AH = 2 – 0,5 = 1,5 и OH/BH = BH/AH; BH²= OH * AH; BH²= 0,5 * 1,5 = 0,75.
Или:
2) △OBA – прямоугольный. Т.к. OB = 1/2AO, то ∠A = 30°. Значит ∠BOA = 60°.
OB = OM и ∠BOA = 60° ⟹ △OBM – равносторонний, BH – высота. h = a√3/2.
BH= OM*√3/2; BH = 1*√3/2; BH²= (√3/2)²= 3/4 = 0,75.
Или:
2) △OBA – прямоугольный; BH – высота; S = OB*AB/2 и S = OA*BH/2.
Значит OB*AB = OA*BH; BH = OB*AB/OA; BH = 1*√3/2; BH²= (√3/2)²= 3/4 = 0,75.