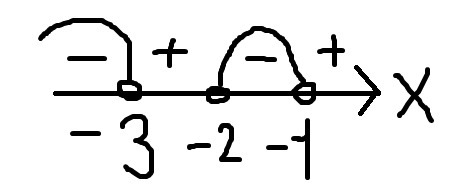1 \\ \\ ODZ: (x+1)(x+2)(x+3) \ne 0 \ ; \ x \ne -1 \ , \ x \ne -2 \ , \ x \ne -3 \\ \\ \dfrac{(x-1)(x-2)(x-3)}{(x+1)(x+2)(x+3)} - \dfrac{(x+1)(x+2)(x+3)}{(x+1)(x+2)(x+3)} > 0 \\ \\ \dfrac{(x-1)(x-2)(x-3) - (x+1)(x+2)(x+3)}{(x+1)(x+2)(x+3)} > 0 \\ \\ \dfrac{x^{3}-6x^{2} + 11x -6 -(x^{3} + 6x^{2}+11x+6) }{(x+1)(x+2)(x+3)} > 0 \\ \\ \dfrac{x^{3}-6x^{2} + 11x -6 - x^{3} - 6x^{2}-11x-6 }{(x+1)(x+2)(x+3)} > 0 \\ \\ \dfrac{-12x^{2} - 12}{(x+1)(x+2)(x+3)} > 0 \ / * (-1) " alt=" \dfrac{(x-1)(x-2)(x-3)}{(x+1)(x+2)(x+3)} > 1 \\ \\ ODZ: (x+1)(x+2)(x+3) \ne 0 \ ; \ x \ne -1 \ , \ x \ne -2 \ , \ x \ne -3 \\ \\ \dfrac{(x-1)(x-2)(x-3)}{(x+1)(x+2)(x+3)} - \dfrac{(x+1)(x+2)(x+3)}{(x+1)(x+2)(x+3)} > 0 \\ \\ \dfrac{(x-1)(x-2)(x-3) - (x+1)(x+2)(x+3)}{(x+1)(x+2)(x+3)} > 0 \\ \\ \dfrac{x^{3}-6x^{2} + 11x -6 -(x^{3} + 6x^{2}+11x+6) }{(x+1)(x+2)(x+3)} > 0 \\ \\ \dfrac{x^{3}-6x^{2} + 11x -6 - x^{3} - 6x^{2}-11x-6 }{(x+1)(x+2)(x+3)} > 0 \\ \\ \dfrac{-12x^{2} - 12}{(x+1)(x+2)(x+3)} > 0 \ / * (-1) " align="absmiddle" class="latex-formula">
0 \\ \\ \dfrac{1}{(x+1)(x+2)(x+3)} < 0 \ (1) \\ \\ x\in (-\infty ; -3)\cup (-2;-1) " alt=" \dfrac{12x^{2} + 12}{(x+1)(x+2)(x+3)} < 0 \\ \\ \dfrac{12(x^{2} + 1)}{(x+1)(x+2)(x+3)} < 0 \ / * 12(x^{2} + 1) \ , \ T.K. \ 12(x^{2} + 1) > 0 \\ \\ \dfrac{1}{(x+1)(x+2)(x+3)} < 0 \ (1) \\ \\ x\in (-\infty ; -3)\cup (-2;-1) " align="absmiddle" class="latex-formula">
Ответ: x ∈ (-∞ ; -3)∪(-2;-1)
