Из точки М ** основании АВ треугольника АВС проведены прямые параллельно двум другим...

Question

Из точки М на основании АВ треугольника АВС проведены прямые параллельно двум другим сторонам. Площадь отсекаемого ими параллелограмма равна 5/18 площади треугольника. Найти отношение, в котором точка М делит прямую АВ (АМ/МВ)

Comments

Очень прошу решение без чистой алгебры

---

Без алгебры не получится.

---

Можно угадать ответ. Параллелограмм разделен на 5 единичных частей - это параллелограммы, способ их размещения - 1:5. Параллельные линии делят стороны угла в одинаковом отношении.

Answer 1

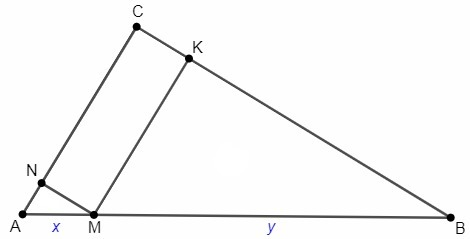
AM=x, BM=y

S(AMN)+S(MBK) = (1 -5/18) S(ABC) =13/18 S(ABC)

Параллельные прямые отсекают от угла подобные треугольники.

△AMN~△ABC, △MBK~△ABC

Площади подобных треугольников относятся как квадрат коэффициента подобия.

S(AMN)/S(ABC)= (x/(x+y))^2

S(MBK)/S(ABC)= (y/(x+y))^2

(x^2+y^2)/(x+y)^2 =13/18 <=>

18(x^2+y^2) = 13(x^2+y^2) +26xy <=>

x^2 -5,2xy +y^2 =0 <=> | ÷y^2

t=x/y: t^2 -5,2t +1 =0 <=> t₁,₂= 2,6±√(6,76-1) =2,6±2,4 <=> t₁=5; t₂=1/5

Ответ: M делит AB в отношении 1:5

---