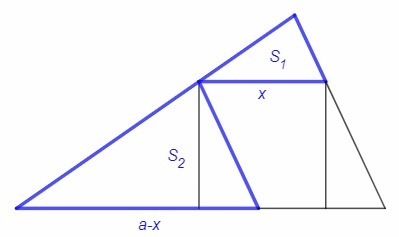
S - площадь треугольника, x - сторона квадрата.
Сторона квадрата, параллельная основанию треугольника, отсекает подобный треугольник с основанием x и площадью S1. Стороны квадрата, перпендикулярные основанию треугольника, отсекают треугольники, из которых складывается подобный треугольник с основанием a-x и площадью S2.
Площади подобных треугольников относятся как квадрат коэффициента подобия.
S1/S = x^2/a^2
S2/S = (a-x)^2/a^2
S1+S2 =5/6 S
(S1+S2)/S = (x^2 + (a-x)^2)/a^2 <=>
5/6 = (2x^2 -2ax +a^2)/a^2 <=>
12x^2 -12ax +6a^2 = 5a^2 <=>
x^2 -ax +a^2/12 =0 <=>
x1,2= (a+-√(a^2 -a^2/3))/2 =a(1+-√(2/3))/2 =a(3+-√6)/6
xa(3-√6)/6