sinx
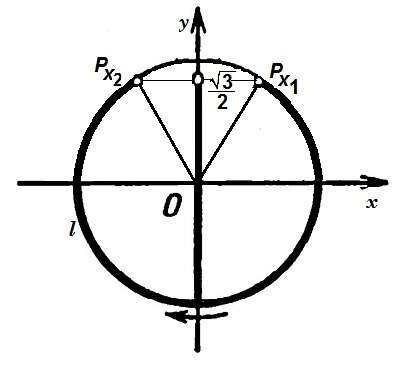
Это неравенство означает, что все точки Рх единичной окружности при значениях х, удовлетворяющих данному неравенству, имеют ординату, меньшую √3/2. Множество всех таких точек - дуга l, выделенная на рисунке. Концы её Рx1 и Рх2 не входят в рассматриваемое множество, поскольку их ординаты не меньше, а равны √3/2. Чтобы найти условие, при котором точка Рх принадлежит указанному множеству, найдём х1 и х2. Возьмём х1=arcsin√3/2=π/3.
Рассмотрим обход дуги l от точки Рх1 и Рх2, в направлениии по часовой стрелке; х2
-4π/3+2πn
Ответ: -4π/3+2πn