Необходимо подробное решение. Желательно на листочке от руки.

Касательно первого задания, я не люблю решать подобные системы методом их сведения к дифф. уравнению более высокого порядка... Я предпочитаю метод собственных значений и собственных векторов матрицы системы... Тогда

$\left[\begin{array}{ccc}1&-3\\3&1\end{array}\right]$ - матрица системы

Найдем собственные значения:

$\lambda^2-2\lambda+10=0$

$\lambda=1\pm 3i$

Т.е. это пара комплексно сопряженных чисел, достаточно найти собственный вектор отвечающий одному из них, к примеру тому что с плюсом:

$\left[\begin{array}{ccc}i\\1\end{array}\right]$ - наш СВ

Далее, общее решение исходной системы записывается в виде

$\left[\begin{array}{ccc}x(t)\\y(t)\end{array}\right] =C_1*Re( \left[\begin{array}{ccc}i\\1\end{array}\right] *e^{(1+3i)*t)})+C_2*Im( \left[\begin{array}{ccc}i\\1\end{array}\right] *e^{(1+3i)*t)})$

Откуда

$\left[\begin{array}{ccc}x(t)\\y(t)\end{array}\right] = C_1*e^t*\left[\begin{array}{ccc}-Sin(3t)\\Cos(3t)\end{array}\right] + C_2*e^t*\left[\begin{array}{ccc}Cos(3t)\\Sin(3t)\end{array}\right]$

Что и будет ответом (если я не ошибся в расчетах)

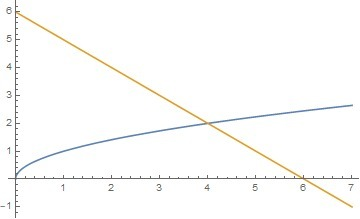
Во втором задании удобно нарисовать график всех этих функций (прикр. файлы). Из него видно, что на отрезке от 0 до 4 по оси x нужная область ограничена снизу кривой $\sqrt{x}$ , сверху прямой $6-x$ Тогда исходный интеграл запишется как
$\int\limits^4_0 {} \, dx \int\limits^b_a {f(x,y)} \, dy$