Рассмотрим систему и то третье неравенство, представим что везде стоят знаки равенства, построим соотв. графики.
Домножим первое уравнение системы на двойку, приравняем ко второму, получим


Это будет прямая, целиков состоящая из точек пересечения графиков уравнений системы при разных значениях параметра. Если хотите, точка пересечения "скользит" по этой прямой при разных a
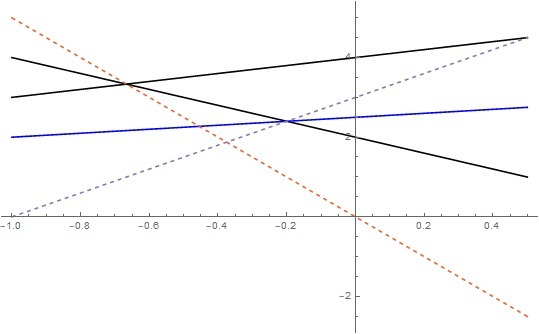
Как именно скользит? При уменьшении a очевидно смещается вниз. В прикрепленном файле графики уравнений системы нарисованы как черные линии, прямая их скольжения как оранжевая пунктирная линия.
Теперь рассмотрим то третье уравнение. Его график показан как голубая линия, он пересекается с графиком одного из уравнений системы. Нас интересует как ведет себя точка пересечения в зависимости от параметра a Аналогично находим прямую скольжения, она задается как  На графике эта прямая показана как голубая пунктирная линия. При уменьшении a точка пересечения съезжает по ней вниз.
На графике эта прямая показана как голубая пунктирная линия. При уменьшении a точка пересечения съезжает по ней вниз.
Далее, теперь опять считаем что нам даны неравенства. Все, что лежит выше ломаной (или на ней), образованной двумя черными прямыми - решение системы. Все что выше голубой линии (строго выше) - решение третьего неравенства. Случай, показанный в прикрепленном файле, соответствует поставленной задаче: каждое решение системы является решение того неравенства.
Граничным значением параметра будет то, при котором все три прямые пересекутся в 1 точке (точке пересечения пунктирных прямых). Мы знаем уравнения пунктирных прямых, не сложно найти точку их пересечения 
Подставим в любое из уравнений, получим 
Таким образом, при  9/8 " alt=" a>9/8 " align="absmiddle" class="latex-formula"> каждое решение системы будет решением неравенства.
9/8 " alt=" a>9/8 " align="absmiddle" class="latex-formula"> каждое решение системы будет решением неравенства.
Почему не подходит a=9/8 ? Потому что при таком параметре точка пересечения всех трех кривых будет решением системы (там нестрогое неравенство), но не будет решением третьего неравенства (она лежит на прямой, а надо чтоб была строго выше этой прямой)