Внутри квадрата дана точка, расстояния от которой до некоторых трех вершин квадрата равны...

Question

Внутри квадрата дана точка, расстояния от которой до некоторых трех вершин квадрата равны 3, 4, 5. Докажите, что эта точка не может лежать на диагонали квадрата.

Answer 1

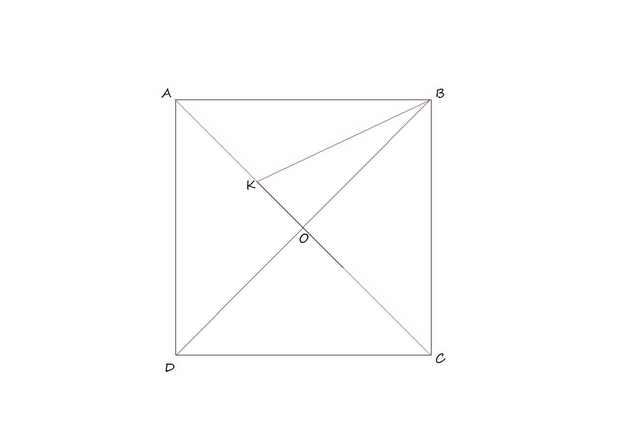
Предположим противное: пусть эта точка лежит на диагонали квадрата. Раз все расстояния разные, то рассматривать случай с вершинами D, B, A или D, B, C нет смысла, поскольку KD=KB; Поэтому рассмотрим случай на рисунке. Пусть KO = x; Тогда x = (AK+KC)/2; Значит x может быть равен 4, 3,5, 4,5. KB - гипотенуза. Т.е. KB>KO=x; При x=4 это не выполняется. При x=4,5 также не выполняется. При x=3,5 используя теорему Пифагора приходим к тому, что OB - иррационально, хотя OB=OC=4-3,5=0,5

---

Comments

у меня ошибка: x=(kc-ak)/2; Тогда x= 0,5 или 1. первый случай: х=0.5. половина диагонали равна 4.5. гипотенуза равна 3. не выполняется нераенство. треугольника: 3+0,5>4,5 . противоречие. с х=1 аналогично.