Через вершины а и в треугольника авс проведена окружность пересекающая стороны вс и ас в...

Question

Через вершины а и в треугольника авс проведена окружность пересекающая стороны вс и ас в точках в и е соответственно.Найдите радиус этой окружности если площадь треугольника cde в 2 раза меньше площади четырехугольника abde ab=15 угол c =30 градусов

Comments

ошибка в условии

---

5√3

Answer 1

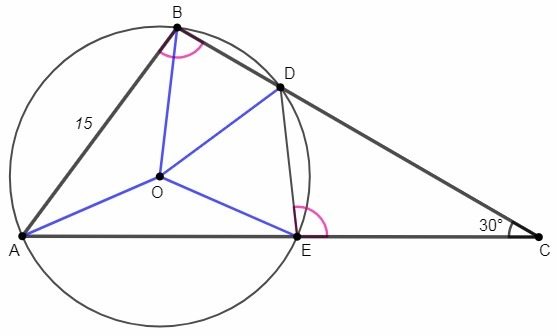
∠ABD+∠AED=180° (противоположные углы вписанного четырехугольника)

∠CED=180°-∠AED =∠ABD

△ABC~△DEC (по двум углам)

S(ABC)/S(DEC) =3 <=> AB/DE =√3 (площади подобных треугольников относятся как квадрат коэффициента подобия)

∪AB/2 -∪DE/2 =30° (угол между секущими)

По формуле длины хорды

AB= 2R sin(∪AB/2)

DE= 2R sin(∪DE/2)

∪DE/2=x

sin(x+30°)/sinx =√3 <=>

(sinxcos30° +cosxsin30°)/sinx =√3 <=>

√3/2 +ctgx/2 =√3 <=>

ctgx= √3 <=> x=30°

∪DE=60° => ∠DOE=60° => △DOE - равносторонний, DO=DE

r= DE =AB/√3 =15/√3 =5√3  ~8,66

---