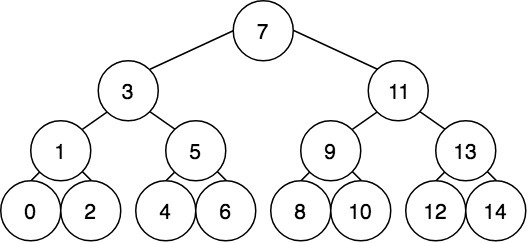
Дерево Фенвика для массива A можно себе представлять так, как изображено на прикрепленном рисунке. В вершине, помеченной числом i, хранится сумма A[i] и всех элементов массива A с индексами, которые записаны в левом поддереве вершины i. Например, Fenwick[11] = A[8] + A[9] + A[10] + A[11]. Дерево Фенвика устроено так, чтобы в каждой вершине Fenwick[n] хранилась сумма отрезка массива от некоторого F(n) до n, нужно сообразить, чему равно F(n). F(n) получается, если идти по дереву в левые поддеревья, пока не наткнёмся на лист, он помечен чётным числом. Если двоичная запись числа n оканчивается на k единиц, то в F(n) эти k единиц заменены на нули.
Пусть нужно вычислить сумму префикса A[0..n], например, n = 9. Глядя на дерево, можно сообразить, что эта сумма равна (A[0] + A[1] + ... + A[7]) + (A[8] + A[9)) = Fenwick[7] + Fenwick[9]. В такой сумме обязательно есть Fenwick[n]: A[0] + A[1] + ... + A[n] = (A[0] + ... + A[F(n) - 1]) + (A[F(n)] + ... + A[n]) = (A[0] + ... + A[F(n) - 1]) + Fenwick[n]. Сумму в скобках тоже можно представить в виде суммы Fenwick[...].
Обновление значения A[n] приводит к обновлению некоторых Fenwick[k], а именно, Fenwick[n], и затем всех вершин-родителей, для которых текущая вершина является левым потомком. Например, чтобы обновить A[9], придется обновить Fenwick[9] и Fenwick[11]. Посчитано, что если текущая вершина имеет номер k, то следующая имеет номер k | (k + 1), и так далее, пока не кончатся вершины.
Высота дерева O(log n), так что операции нахождения суммы и обновления элементов работают за O(log n).