В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу в отношении 3:2....

Question

В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу в отношении 3:2. Найдите отношения проекций катетов на гипотенузу.

Comments

3 к 2

---

Можете подробнее описать

---

биссектриса делит гипотенузу на части, пропорциональные катетам

---

подождите немного...

---

9 к 4....

---

судя по ответу-есть наверное и более короткое решение

---

Спасибо!)

Answer 1

один катет 3х, другой 2х

Тогда гипотенуза x√13

---

Answer 2

Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.

a/b =3/2 (a, b - катеты).

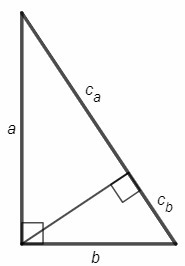
Высота из прямого угла делит гипотенузу на отрезки Ca=a^2/c; Cb=b^2/c (Сa, Cb - проекции катетов).

Ca/Cb =a^2/b^2 =(3/2)^2 =9/4

---

Comments

Высота из прямого угла делит гипотенузу на отрезки Ca=a^2/c; Cb=b^2/c -это откуда?

---

Высота из прямого угла делит треугольник на подобные друг другу и исходному, c/a=a/Ca => катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу, a^2=Ca*c.

---

спасибо