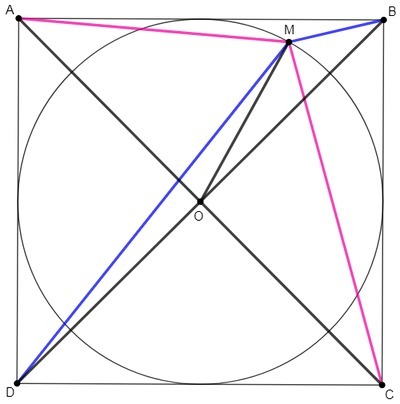
Точка пересечения диагоналей квадрата является центром вписанной и описанной окружностей. Радиусы вписанной и описанной окружностей квадрата относятся как катет и гипотенуза в равнобедренном прямоугольном треугольнике, R=r√2.
MO=r =5
AO=BO=CO=DO =r√2
По теореме Аполлония
△AMC: AM^2 + CM^2 = 2(MO^2 + AO^2)
△BMD: BM^2 + DM^2 = 2(MO^2 + BO^2)
AM^2 + CM^2 + BM^2 + DM^2 = 4(MO^2 +AO^2) =12r^2 =12*25=300
___________________________________________________
Теорема Аполлония:
a^2 +b^2 = 2(Mc^2 +(c/2)^2), Mc - медиана к стороне с.