Доказать можно графически, но рассматривать графики функций y=10ˣ и у=х¹⁰ не разумно, так как обе эти функции быстро растут, поэтому перепишем данное уравнение (прологарифмируем его по основанию 10)

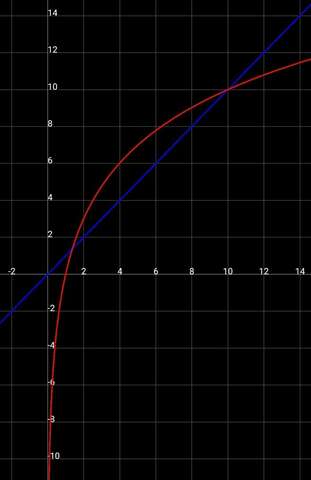
а уж теперь строим графики у=х и у=10lg|x| или только для доказательство того, что есть корень 10 (х>0) модуль у логарифма можно опустить (пренебрегая отрицательным корнем).
После чего получаем пересение в точке 10. Что и требовалось доказать