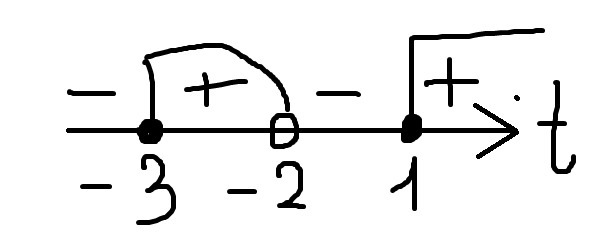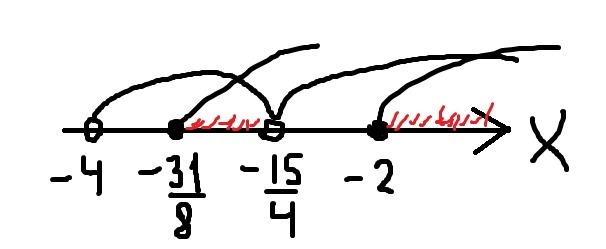Помогите с решением! log_2(x+4)>=log_(4x+16)(8)

Question

Дан 1 ответ

Правильный ответ

0 \\ 4x+16 > 0 \\ 4x + 16 \ne 1 \end{gathered} \right.$ \ ; \ $\left\{ \begin{gathered} x > -4 \\ x \ne -\dfrac{15}{4} \\ \end{gathered} \right.$ \ ; \ x \in (-4;-\dfrac{15}{4})\cup ( -\dfrac{15}{4}; +\infty) " alt=" \log_{2}(x+4) \ge \log_{(4x+16)}8 \\ \\ ODZ: \ $\left\{ \begin{gathered} x + 4 > 0 \\ 4x+16 > 0 \\ 4x + 16 \ne 1 \end{gathered} \right.$ \ ; \ $\left\{ \begin{gathered} x > -4 \\ x \ne -\dfrac{15}{4} \\ \end{gathered} \right.$ \ ; \ x \in (-4;-\dfrac{15}{4})\cup ( -\dfrac{15}{4}; +\infty) " align="absmiddle" class="latex-formula">

$\log_{2}(x+4) \ge \dfrac{1}{\log_{8}(4x+16)} \\ \\ \log_{2}(x+4) \ge \dfrac{1}{\frac{1}{3}\log_{2}(4x+16)} \\ \\ \log_{2}(x+4) \ge \dfrac{3}{\log_{2}(4(x+4))} \\ \\ \log_{2}(x+4) \ge \dfrac{3}{\log_{2}(4) + \log_{2}(x+4)} \\ \\ \log_{2}(x+4) \ge \dfrac{3}{2 + \log_{2}(x+4)} \\ \\ \log_{2}(x+4) = t \\ \\ t \ge \dfrac{3}{2+t} \\ \\ \dfrac{t^{2}+2t-3}{2+t} \ge 0 \\ \\ \dfrac{(t-1)(t+3)}{2+t} \ge 0 \ (1)$

$\left[ \begin{gathered} -3 \le t < -2 \\ t \ge 1 \\ \end{gathered} \right.$

$\left[ \begin{gathered} -3 \le \log_{2}(x+4) < -2 \\ \log_{2}(x+4) \ge 1 \\ \end{gathered} \right.$

$\left[ \begin{gathered} $\left\{ \begin{gathered} \log_{2}(x+4) \ge -3 \\ \log_{2}(x+4) < -2 \\ \end{gathered} \right.$ \\ \log_{2}(x+4) \ge 1 \\ \end{gathered} \right.$

$\left[ \begin{gathered} $\left\{ \begin{gathered} \log_{2}(x+4) \ge \log_{2}2^{-3} \\ \log_{2}(x+4) < \log_{2}2^{-2} \\ \end{gathered} \right.$ \\ \log_{2}(x+4) \ge \log_{2}2^{1} \\ \end{gathered} \right.$

$\left[ \begin{gathered} $\left\{ \begin{gathered} x+4 \ge 2^{-3} \\ x+4 < 2^{-2} \\ \end{gathered} \right.$ \\ x+4 \ge 2 \\ \end{gathered} \right.$

$\left[ \begin{gathered} $\left\{ \begin{gathered} x \ge -\dfrac{31}{8} \\ x < -\dfrac{15}{4} \\ \end{gathered} \right.$ \\ x \ge -2 \\ \end{gathered} \right.$

$x \in [-\dfrac{31}{8}; -\dfrac{15}{4}) \cup [-2;+\infty)$

С учётом ОДЗ (2):

$x \in [-\dfrac{31}{8}; -\dfrac{15}{4}) \cup [-2;+\infty)$

Ответ: x ∈ [-31/8; -15/4)∪ [-2; +∞)

InvisorTech_zn (8.9k баллов) 10 Сен, 18