К графику функции y=1+1/x в точке М (1, 2) проведена касательная. Найдите длину отрезка...

Question 1

К графику функции y=1+1/x в точке М (1, 2) проведена касательная. Найдите длину отрезка касательной, заключенной между осями координат. Сделайте схематический чертеж.

Question 2

$y=1+\dfrac{1}{x}; \ \ \ M=(1 \ ;2)$

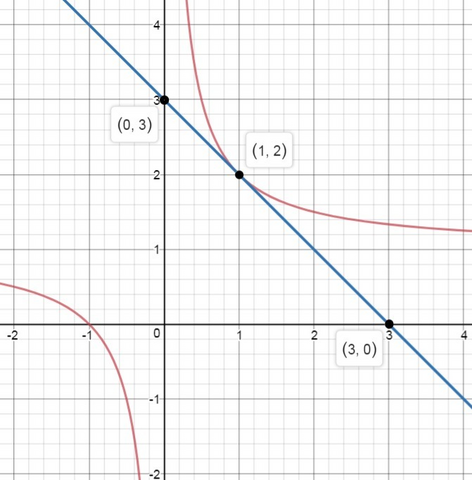
Найдем уравнение касательной

$y'=-\dfrac{1}{x^2}$

$y_{kac}=1+1+(-\dfrac{1}{1})\cdot(x-1)=3-x$

График касательной пересекает ось x в точке

$3-x=0 \ \Rightarrow \ x=3$

и так как коэффициент наклона k=-1, то касательная параллельна прямой y=-x и пересекает ось y в точке (0; 3)

Из равнобедренного прямоугольного треугольника с катетами по 3

$c=\sqrt{3^2+3^2}=3\sqrt{2}$

Ответ: 3√2

NeZeRAvix_zn · Answer 1 · 2018-09-10T02:22:49+0000