Угловые коэффициенты у прямых равны (у данной в задаче и у параллельных ей).
Если касательные параллельны прямой y=4x+3, то угловой коэффициент k=4.
А производная уже самой функции равна угл. коэф-ту k к графику функции y=4x+3.
Находим производную функции y=1+3sin((2/3)x)-2sin(x):
y'=2cos((2/3)x)-2cos(x)
y'=k, тогда
2cos((2/3)x)-2cos(x)=4
cos((2/3)x)-cos(x)=2
Разделим уравнение на две функции
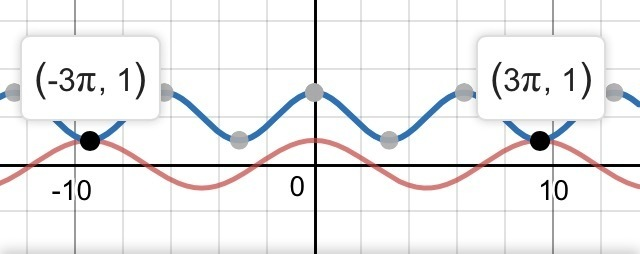
y=cos(2x/3), y=cos(x)+2 и решим его графически.
Получаем конечный ответ: x=3π+6πk (k∈Z).