окончательно имеем дело с системой  (домножили неравенство системы на
(домножили неравенство системы на  0} " alt=" \mathtt{x^2-2x+4=(x-1)^2+3>0} " align="absmiddle" class="latex-formula">; также учитываем, что
0} " alt=" \mathtt{x^2-2x+4=(x-1)^2+3>0} " align="absmiddle" class="latex-formula">; также учитываем, что  — корень второй кратности, поэтому при переходе через него на числовой прямой знак неравенства не меняется)
— корень второй кратности, поэтому при переходе через него на числовой прямой знак неравенства не меняется)
найдём корни квадратного трёхчлена, чтобы разложить всё неравенство на множители:
 , следовательно,
, следовательно, 
 ; получается,
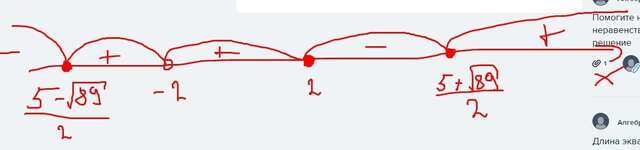
; получается, ![\mathtt{x\in[\frac{5-\sqrt{89}}{2};-2)U(-2;2]U[\frac{5+\sqrt{89}}{2};+\infty)} \mathtt{x\in[\frac{5-\sqrt{89}}{2};-2)U(-2;2]U[\frac{5+\sqrt{89}}{2};+\infty)}](https://tex.z-dn.net/?f=+%5Cmathtt%7Bx%5Cin%5B%5Cfrac%7B5-%5Csqrt%7B89%7D%7D%7B2%7D%3B-2%29U%28-2%3B2%5DU%5B%5Cfrac%7B5%2B%5Csqrt%7B89%7D%7D%7B2%7D%3B%2B%5Cinfty%29%7D+) (решение неравенства методом интервалов в приложении) и, следовательно, наименьшее целое решение равно –1 (решение
(решение неравенства методом интервалов в приложении) и, следовательно, наименьшее целое решение равно –1 (решение  , очевидно, не является целым)
, очевидно, не является целым)
Ответ: –1