|x| + 2|y - 1| = b
x ≥ 0
y ≥ 1
x + 2y - 2 = b ⇒ y = -x/2 + 1 + b/2 (1)
x ≥ 0
y < 1
x - 2y + 2 = b ⇒ y = x/2 + 1 - b/2 (2)
x < 0
y ≥ 1
-x + 2y - 2 = b ⇒ y = x/2 + 1 + b/2 (3)
x < 0
y < 1
-x - 2y + 2 = b ⇒ y = -x/2 + 1 - b/2 (4)
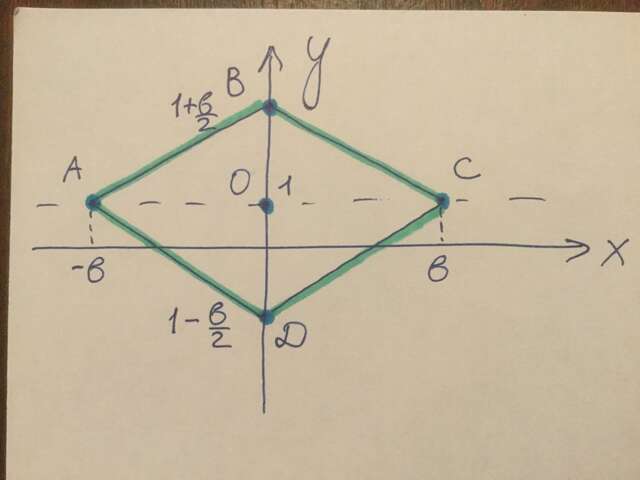
Приравнивая (3) и (4), получаем Ха = -b. ⇒ A (-b; 1)
Приравнивая (1) и (2), получаем Хc = b. ⇒ C (b; 1)
Подставляя в (1) х = 0, получаем Yb = 1 + b/2. ⇒ B (0; 1 + b/2)
Подставляя в (2) х = 0, получаем Yd = 1 - b/2. ⇒ D (0; 1 - b/2)
ABCD - параллелограмм.
Его диагонали равны: АС = 2b, BD = b.
Сторона параллелограмма: ВС = √(ОВ² + ОС²) = √((b/2)² + b²) = b√5/2.
Диаметр вписанной окружности будет высотой параллелограмма.
Выразим площадь параллелограмма дважды: один раз через диагонали, второй - через сторону и проведенную к ней высоту:
S (ABCD) = 2b·b/2 = b√5/2 · 2·2√5
Откуда: b = 10.