Помогите решить!! Объём шара равен 6. Найдите объём цилинра , ВПИСАННОГО в шар.

Question

Дан 1 ответ

Правильный ответ

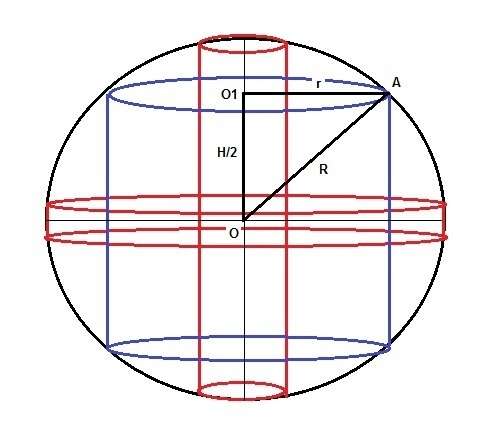
В шар можно вписать много разных цилиндров, несколько из них показано на рисунке. Обозначим r радиус цилиндра, H высоту. R радиус шара.

В крайних положениях, при R = r и при H = 2R будет объем цилиндра V(ц) = 0.

Близкие к этому положения показаны красным.

В некотором положении объем цилиндра будет максимальным.

Это положение показано синим.

Объем шара V(ш) = 4/3*pi*R^3 = 6

R^3 = 6*3/(4pi) = 9/(2pi) = 27/(6pi)

R = ∛(27/(6pi)) = 3/∛(6pi)

По теореме Пифагора (треугольник показан черным)

(H/2)^2 + r^2 = R^2 = 9/∛(36pi^2)

$r^2=\frac{9}{\sqrt[3]{36\pi^2}} -\frac{H^2}{4} =\sqrt[3]{\frac{9^3}{9*4\pi^2}} -\frac{H^2}{4} =\sqrt[3]{\frac{81}{4\pi^2}}-\frac{H^2}{4}$

Объем цилиндра

$V=\pi r^2H=\pi (\sqrt[3]{\frac{81}{4\pi^2}}-\frac{H^2}{4})H=\pi H\sqrt[3]{\frac{81}{4\pi^2}}-\frac{\pi}{4} H^3=H\sqrt[3]{\frac{81\pi}{4}}-\frac{\pi}{4} H^3$

Объем будет максимальным, когда производная будет равна 0

$V'(H)=\sqrt[3]{\frac{81\pi}{4}}-\frac{3\pi}{4} H^2=0$

$H^2=\sqrt[3]{\frac{81\pi}{4}}:\frac{3\pi}{4}=\sqrt[3]{\frac{81\pi}{4}*\frac{64}{27\pi^3}}=\sqrt[3]{\frac{3*16}{\pi^2}}=\sqrt[3]{\frac{48}{\pi^2}}$

$H=\sqrt[6]{\frac{48}{\pi^2}}$

Теперь найдем радиус цилиндра

$r^2=\sqrt[3]{\frac{81}{4\pi^2}}-\frac{H^2}{4} =\sqrt[3]{\frac{81}{4\pi^2}}-\frac{1}{4}\sqrt[3]{\frac{48}{\pi^2}}=\sqrt[3]{\frac{81}{4\pi^2}}-\sqrt[3]{\frac{48}{64\pi^2}}=$

$=\sqrt[3]{\frac{81}{4\pi^2}}-\sqrt[3]{\frac{3}{4\pi^2}} =\frac{\sqrt[3]{81}-\sqrt[3]{3}}{\sqrt[3]{4\pi^2}}= \frac{3 \sqrt[3]{3} - \sqrt[3]{3} }{ \sqrt[3]{4 \pi^2 } } = \frac{2 \sqrt[3]{3} }{\sqrt[3]{4 \pi^2 } } = \sqrt[3]{ \frac{8*3}{4 \pi^2 } } = \sqrt[3]{ \frac{6}{\pi^2} }$
Объем цилиндра
$V=\pi r^2H=\pi \sqrt[3]{ \frac{6}{ \pi ^2} } *\sqrt[6]{\frac{48}{\pi^2}} = \sqrt[6]{ \frac{36 \pi ^6}{ \pi ^4} } *\sqrt[6]{\frac{48}{\pi^2}} =\sqrt[6]{36*48} = \sqrt[6]{6^3*8} =\sqrt{12}$

mefody66_zn (320k баллов) 10 Сен, 18