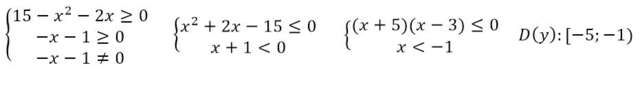Добрый день! Начнём по порядку.
А3:
Задача связана с параллельным переносом гиперболы. Тут всё просто:
1) Раз x = -3 выкл. => при x = -3 функция y(x) не определена. Такое может быть только в 1) 3) 4) Варианте ответа. Далее смотрим на горизонтальную асимптоту. и Видим что она равна 1 => Вариант либо 1) либо 3) Но так как гипербола расположена во II и IV четвертях => 1/x < 0 а такое только в варианте ответа 1)
Ответ: 1)
А4:
Множеством значений функции y = f(x) на интервале X называют множество всех значений функции, которые она принимает при переборе всех x принадлежащих ОДЗ
Легко видим, что y = c + f(x), где с - действительное число (Если точнее натуральное), а f(x) - монотонно возрастающая функция. => y(x) Монотонно убывает. (грубо говоря при x → ∞ y(x) → -∞) Следовательно максимум y(x) = с, т.к f(x)>=0
E(y) = (-∞; 5]
Ответ: 2
А5:
Нахождение D(y) сводиться к решению простой системы
Смотреть фото 1
D(y) [-5; -1]
Ответ: 3
A6:
Здесь думаю, решение писать не стоит, т.к решать модульные неравенства можно многими способами. После решения производим отбор согласно заданному отрезку.
И видим, что целых решений на данном отрезке 4 - это -2; -1; 0; 1
Ответ: 4
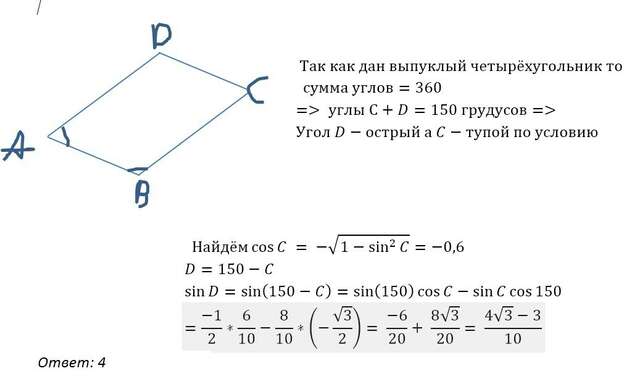
A7:
Как уже отметил человек выше, если у вас есть таблица Брадиса (или либая другая с sin cos и тд), то всё элементарно, но я сильно сомневаюсь, что на экзамене она разрешена.
Поэтому будем решать иначе.
См фото 2
Ответ: 4
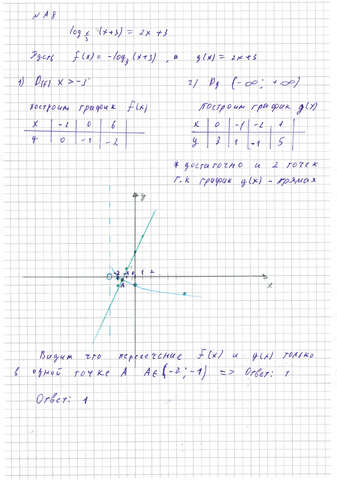
А8:
на мой взгляд решать данный вариант следует именно с этой задачи, она позволит вкл мозги и настроиться на работу с графиками.
См фото 3
Вот как то так! Время решения 18 минут. Удачи! Надеюсь не поздно.