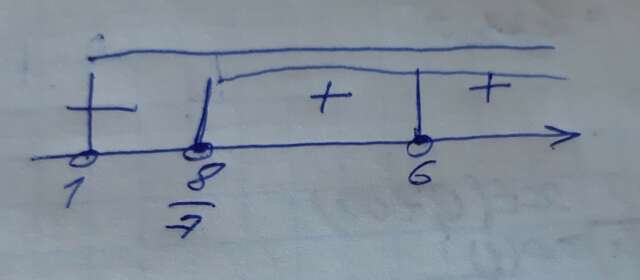
0 \\ odz \\ \: x - 1 > 0 \\ x > 1 \\ {(x - 6)}^{2} (1 - log_{ \frac{1}{7} }(x - 1) ) = 0 \\ {(x - 6)}^{2} = 0 \: \: \: \: and \: \: \: 1 - log_{ \frac{1}{7} }(x - 1) = 0 \\ x = 6 \: \: and \: \: \: log_{ \frac{1}{7} }(x - 1) = 1 \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: x - 1 = \frac{1}{7 } \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: x = \frac{8}{7} \\ x\in( \frac{8}{7} ;6)\cup(6; + \infty)" alt=" {(x - 6)}^{2} (1 - log_{ \frac{1}{7} }(x - 1) ) > 0 \\ odz \\ \: x - 1 > 0 \\ x > 1 \\ {(x - 6)}^{2} (1 - log_{ \frac{1}{7} }(x - 1) ) = 0 \\ {(x - 6)}^{2} = 0 \: \: \: \: and \: \: \: 1 - log_{ \frac{1}{7} }(x - 1) = 0 \\ x = 6 \: \: and \: \: \: log_{ \frac{1}{7} }(x - 1) = 1 \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: x - 1 = \frac{1}{7 } \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: x = \frac{8}{7} \\ x\in( \frac{8}{7} ;6)\cup(6; + \infty)" align="absmiddle" class="latex-formula">