Металлический конус, площадью боковой поверхности которого равна S, а образующая...

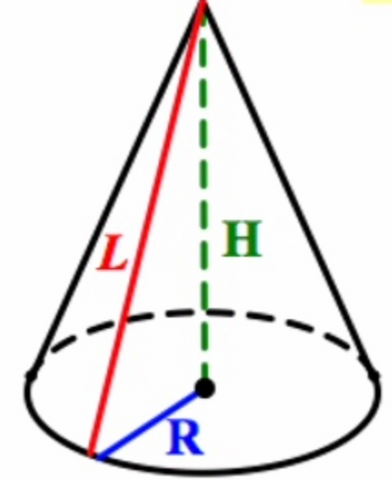
Площадь боковой поверхности:

S=пRL (L - образующая)

Угол a находится между R и L, тогда

cos(a)=R/L <=> R=Lcos(a), отсюда по теореме Пифагора

R²+H²=L² => H²=L²-R² =>

H=√(L²-R²)=√(L²-L²cos²a)=

=√(L²(1-cos²a))=√(L²sin²a)=

=√((Lsin(a))²)=Lsin(a)

Объем конуса равен:

V=(1/3)пR²H=

=(1/3)п•(L²cos²a)•Lsin(a)=

=(1/3)пL³cos²a•sin(a)

Так как S=пRL, то

S/п=RL=L•Lcos(a)=L²cos(a)

Возводим

V=(1/3)пL³cos²a•sin(a) (во 2 степень)

S/п=L²cos(a) (в 3 степень)

<=>

V²=(1/9)п²L⁶cos⁴a•sin²a (1)

S³/п³=L⁶cos³a (2)

Подставляем (2) в (1), получаем:

V²=(S³cos(a)•sin²a)/(9п)

<=>

V=((S•sin(a))/3)•√((S•cos(a))/п)

Объем пирамиды:

V=(1/3)S₁•Hпир, тогда

Hпир=(3V)/S₁=(подставляем V)=

=((S•sin(a))/S₁)•√((S•cos(a))/п)

Ответ:

4) ((S•sin(a))/S₁)•√((S•cos(a))/п)