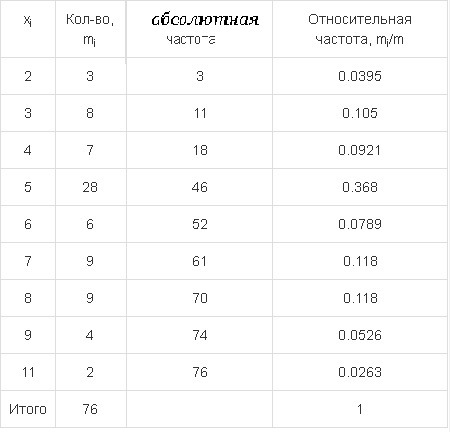
1)  - количество длин букв. Абсолютная частота является целым числом и показывает, сколько раз данное значение повторяется в выборке. Сумма абсолютных частот всегда равна объему выборки.
- количество длин букв. Абсолютная частота является целым числом и показывает, сколько раз данное значение повторяется в выборке. Сумма абсолютных частот всегда равна объему выборки.
В первой ячейке ставим 3 (из количества меньших букв mi=3)
Во второй ячейке 
В третью ячейку 
......
В последней ячейке 
2) Относительная частота ищется по формуле  , где m - объем выборки.
, где m - объем выборки.
В первой ячейке относительной частоты: 3/76=0.0395
Во второй ячейке: 8/76 = 0.105
В третьей ячейке: 7/76 = 0.0921
.....
В последней ячейке: 2/76 = 0.0263
3) Объем: 76. Размах это разность между наибольшим и наименьшим значениями результатов наблюдений: R = 11-2=9.
4) Среднее арифметическое: 
5) Мода - наиболее часто встречающееся значение в выборке. Максимальное значение повторений при x = 5. Следовательно, мода равна 5.
Находим xi, при котором абсолютная частота будет больше ∑m/2 = 39. Это значение xi = 5. Таким образом, медиана равна 5.