При каких значениях параметра a неравенство  a+x " alt=" \sqrt{2-x^{2}}>a+x " align="absmiddle" class="latex-formula"> имеет решения?
a+x " alt=" \sqrt{2-x^{2}}>a+x " align="absmiddle" class="latex-formula"> имеет решения?
ограничения на x:  -a " alt=" x^{2}<2; x>-a " align="absmiddle" class="latex-formula">
-a " alt=" x^{2}<2; x>-a " align="absmiddle" class="latex-formula">
пусть  , тогда:
, тогда:

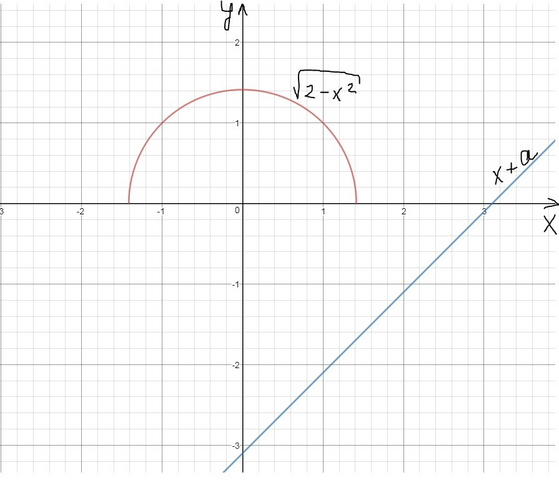
 - график полуокружности, лежащей выше оси x с центром (0;0) и радиусом
- график полуокружности, лежащей выше оси x с центром (0;0) и радиусом 
пусть  - график прямой, проходящей через (0; a), т.е.
- график прямой, проходящей через (0; a), т.е.  смещённый на a вверх-вниз
смещённый на a вверх-вниз
См. вложения (красным цветом -  , синим цветом -
, синим цветом -  )
)
график  должен находиться ниже графика
должен находиться ниже графика 
При  всегда найдётся такой x, что
всегда найдётся такой x, что 
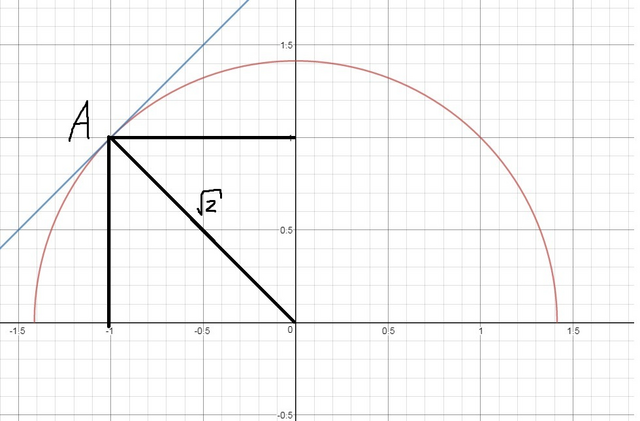
Так будет до касания верхней части окружности (рис.2)
Определим точку касания A:
Её координаты (-1;1), а значит график функции  имеет вид
имеет вид 
Следовательно при всех a<2 <img src="https://tex.z-dn.net/?f=+g%28x%29%3Cf%28x%29++" id="TexFormula17" title=" g(x)<f(x) " alt=" g(x)<f(x) " align="absmiddle" class="latex-formula"> имеет решения
Ответ: