Помогите решить задание ОГЭ 2 часть. №23

$y=1-\frac{2x^4+x^3}{x+2x^2}$

ОДЗ: х+2х² ≠ 0

х(1+2х) ≠ 0

х ≠ 0; х ≠ - 0,5

$y=1-\frac{2x^4+x^3}{x+2x^2}=1-\frac{x^3(2x+1)}{x(1+2x)}=1-x^2=-x^2+1$

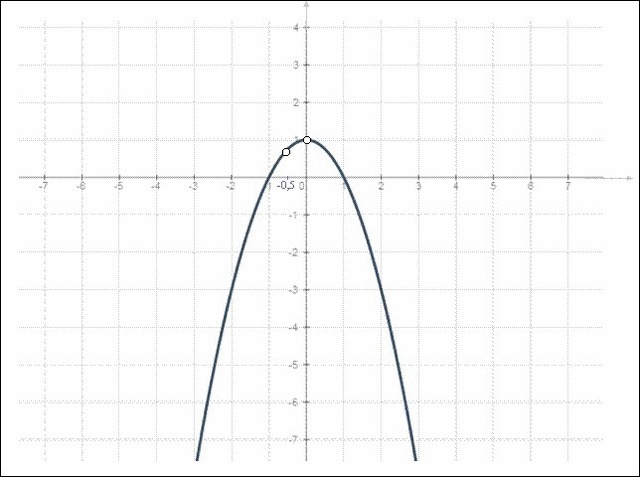
Строим квадратную параболу у = - х² + 1 с проколами

в точках х=0 и х = - 0,5.

При х= - 0,5 находим значение у.

у = -(-0,5)² + 1 = - 0,25+1=0,75;

у = 0,75

Очевидно, что прямая у=n ,будет иметь с графиком две общие точки

при n < 1 , исключая n = 0,75.

n∈ (-∞; 0,75)∪(0,75; 1)