Найдите все положительные значения a, при каждом из которых система имеет единственное...

1-е уравнение задаёт 2 окружности радиуса 2. Центры - $O_{1}(-6;12)$ и $O_{2}(6;12)$

2-е уравнение задаёт окружность радиуса $|a|$ (но в нашей задаче просто a, так как по условию a>0). Центр - $M(-1; 0)$

Решаем графически, когда есть 1 решение:

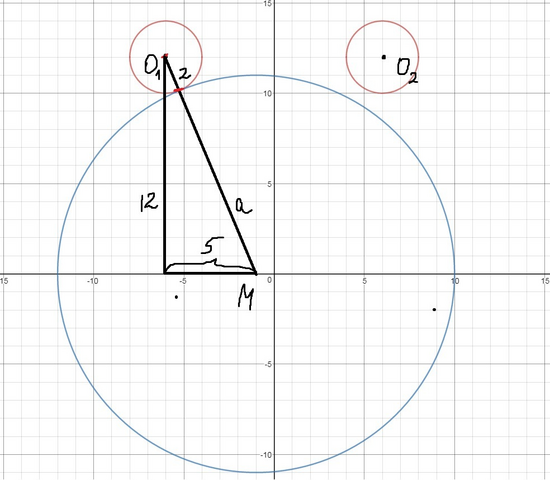
Красным на рисунке 1-е уравнение, синим - 2-е.

1-е решение будет касание левой окружности (т.к. она ближе к точке M)

Опускаем перпендикуляр как на рисунке и по т. Пифагора:

$a+2=\sqrt{12^2+5^2}=\sqrt{13^2}; a=13-2=11$

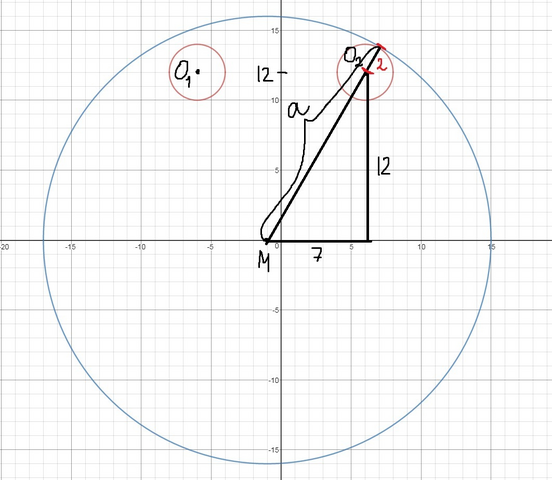
2-е решение (единственное) будет при касании правой красной окружности синей внутренним образом.

Опускаем перпендикуляр как на рисунке и по т. Пифагора:

$a=\sqrt{12^2+7^2}+2=\sqrt{193}+2$

Ответ: $a=11; a=\sqrt{193}+2$