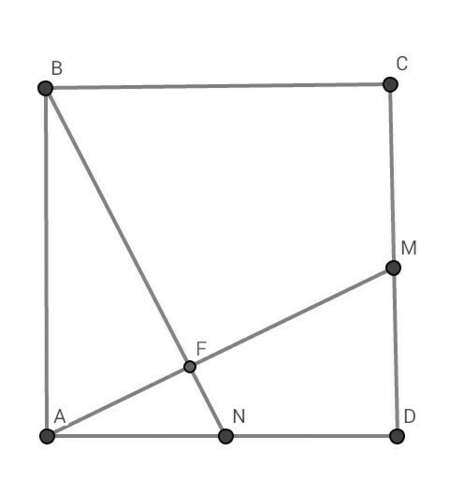
ДАНО: АВCD - квадрат ; АВ = 10 ; СM = MD = 5 ; AN = ND = 5 ; F - точка пересечения прямых АМ и ВN
ДОКАЗАТЬ: FM = 1,5 × AF
_______________________________
РЕШЕНИЕ:
A) 1 способ : Заметим (см. рис. 2), что треугольники АВN и AMD равны по двум катетам ( АВ = АD - стороны квадрата , АN = MD - по условию ). Повернём ВАN на угол 90° против часовой стрелке и совместим точку А с точкой D. Сторона MD совместится со стороной AN, а сторона AD — со стороной AB. Поскольку после поворота на 90° стороны AM и BN совместились, значит, до поворота угол между ними был равен 90°. АМ перпендикулярен BN.
2 способ : ∆ АВN = ∆ AMD по двум катетам ( АВ = АD - стороны квадрата , АN = MD - по условию ).
В равных треугольниках соответственно равные элементы => угол АВN = угол МАD ; угол ВNA = угол AMD
Значит, угол FAN + угол FNA = 90° =>
АМ перпендикулярен BN.
Б) Рассмотрим ∆ АМD :
По теореме Пифагора:
АМ² = АD² + MD² = 10² + 5² = 100 + 25 = 125
AM = 5√5
В ∆ FNA : cos FAN = AF / AN
В ∆ АМD : cos МАD = AD / AM
cos FAN = cos MAD = AF / AN = AD / AM =>
AF = ( AN × AD ) / AM = 5 × 10 / 5√5 = 10/ √5 = 2√5
FM = AM - AF = 5√5 - 2√5 = 3√5
FM / AF = 3√5 / 2√5 = 1,5
Из этого следует, что FM = 1,5 × AF , что и требовалось доказать