10a+√(7+6x-x²)=ax+4
ОДЗ:
7+6x-x²≥0
(7-x)(x+1)≥0
x∈[-1;7]
Значит функция существует лишь на отрезке x∈[-1;7].
Найдем крайние точки графика функции:
При x=-1:
10a+√(7+6•(-1)-(-1)²)=a•(-1)+4
10a=4-a
a=4/11
При x=7:
10a+√(7+6•7-7²)=a•7+4
10a=7a+4
a=4/3
Теперь найдём точки экстремума.
Выражаем a и находим первую производную и приравниваем к 0:
a=(4-√(7+6x-x²))/(10-x)
a'=(4√(7+6x-x²)+7x-37)/((10-x)²•√(7+6x-x²))
Тогда 4√(7+6x-x²)+7x-37=0
4√(7+6x-x²)=37-7x
16(7+6x-x²)=49x²-518x+1369
112+96x-16x²=49x²-518x+1369
65x²-614x+1257=0
(3-x)(65x-419)=0
x=3 и x=419/65 (не подходит после проверки)
Тогда x=3 (единственный экстремум функции)
Подставим значение x=3 в основное уравнение:
10a+√(7+6•3-3²)=a•3+4
10a+4=3a+4
Отсюда a=0.
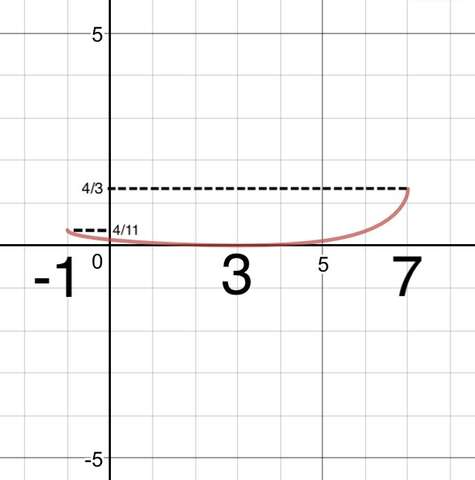
Два "конца" графика уже известны, добавляем третью точку при x=3 (a=0). Она расположена ниже точек 4/11 и 4/3, значит, это точка min функции и через все три точки проводим примерную кривую.
Тогда по графику получаем, что одно решение будет при a∈{0}U(4/11;4/3].
Ответ: a∈{0}U(4/11;4/3].