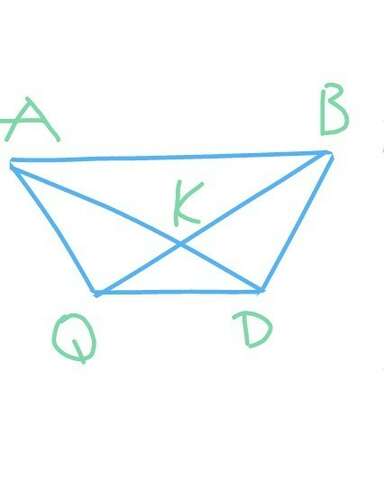
ДАНО: АВ - прямая ; угол QAD = угол DBQ ; угол DAB = угол QBA
ДОКАЗАТЬ: АQ = BD , AD = BQ
_________________________
ДОКАЗАТЕЛЬСТВО:
1) угол QAD = угол DBQ ; угол DAB = угол QBA
Значит, угол BAQ = угол АВD
2) ∆ ВАD = ∆ ABQ по стороне и двум прилежащим углам:
угол BAQ = угол АВD
угол DAB = угол QBA - по условию
АВ - общая сторона
В равных треугольниках соответственно равные стороны:
Значит, AQ = BD , AD = BQ
Что и требовалось доказать.