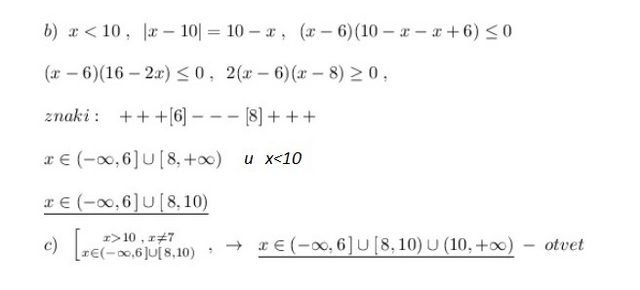Метод рационализации.
0\; ,\; x-6\ne 1}} \right. \; \left \{ {{x\ne 10} \atop {x>6,\; x\ne 7}} \right. \\\\\star \; \; log_{h}f\vee 1\; \; \Leftrightarrow \; \; (h-1)(f-h)\vee 0\; \star \\\\(x-6-1)(|x-10|-(x-6))\leq 0\\\\(x-6)\cdot (|x-10|-x+6)\leq 0\\\\a)\; \; \underline {x>10}\; ,\; \; (x-6)(x-10-x+6)\leq 0\; ,\\\\(x-6)\cdot (-4)\leq 0\; ,\; \; x-6\geq 0\; ,\; \; \underline {x\geq 6}\\\\\left \{ {{x>10} \atop {x\geq 6}} \right.\; \; \to \; \; \underline {x>10}" alt=" log\, _{x-6}|x-10|\leq 1\; ,\; \; \left \{ {{x\ne 10} \atop {x-6>0\; ,\; x-6\ne 1}} \right. \; \left \{ {{x\ne 10} \atop {x>6,\; x\ne 7}} \right. \\\\\star \; \; log_{h}f\vee 1\; \; \Leftrightarrow \; \; (h-1)(f-h)\vee 0\; \star \\\\(x-6-1)(|x-10|-(x-6))\leq 0\\\\(x-6)\cdot (|x-10|-x+6)\leq 0\\\\a)\; \; \underline {x>10}\; ,\; \; (x-6)(x-10-x+6)\leq 0\; ,\\\\(x-6)\cdot (-4)\leq 0\; ,\; \; x-6\geq 0\; ,\; \; \underline {x\geq 6}\\\\\left \{ {{x>10} \atop {x\geq 6}} \right.\; \; \to \; \; \underline {x>10}" align="absmiddle" class="latex-formula">
10\; ,\; x\ne 7} \atop {x\in (-\infty ,6\, ]\cup [\, 8,10)}} \right. \; ,\; \; \to \; \; \underline {x\in (-\infty ,6\, ]\cup [\, 8,10)\cup (10,+\infty )}\; -\; otvet " alt=" b)\; \; x<10\; ,\; \; |x-10|=10-x\; ,\; \; (x-6)(10-x-x+6)\leq 0\\\\(x-6)(16-2x)\leq 0\; ,\; \; 2(x-6)(x-8)\geq 0\; ,\\\\znaki:\; \; \; +++[6]---[8]+++\\\\x\in (-\infty ,6\, ]\cup [\, 8,+\infty )\\\\\underline {x\in (-\infty ,6\, ]\cup [\, 8,10)}\\\\c)\; \; \left [ {{x>10\; ,\; x\ne 7} \atop {x\in (-\infty ,6\, ]\cup [\, 8,10)}} \right. \; ,\; \; \to \; \; \underline {x\in (-\infty ,6\, ]\cup [\, 8,10)\cup (10,+\infty )}\; -\; otvet " align="absmiddle" class="latex-formula">
