1 | В окружности радиуса 1 проведена хорда длины 1. Найти площадь частей круга, **...

Question

1 | В окружности радиуса 1 проведена хорда длины 1. Найти площадь
частей круга, на которые данный круг разделен проведенной хордой.

2 | В прямоугольном треугольнике ABC проведена биссектриса прямого
угла CD, острый угол B равен 30(градусов). Найти углы
треугольника DH1H2, где H1 и H2 - точки пересечения высот
треугольников ACD и BCD.

3 | На стороне AB треугольника ABC взята точка M так, что AM = 2MB, а на стороне AC точка K. Известно, что площадь треугольника AMK в 2 раза меньше площади треугольника ABC. В каком отношении точка K делит сторону AC?

Answer 1

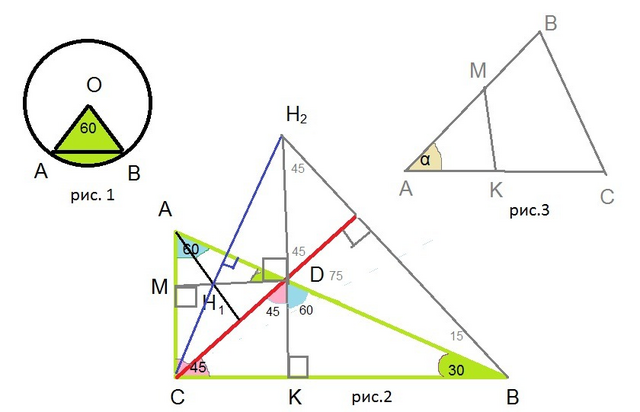
1) См. рис. 1

S(круга)=πR²=π

Треугольник АОВ - равносторонний

AO=OB=R=1

AB=1

Центральный угол АОВ равен 60 °

S₁=S(сек. АОВ)=πR²·360°/60°=(1/6)πR²=(1/6)π

S₂=π-(1/6)π=(5/6)π

2) Cм. рис. Треугольник СDB - тупоугольный, ∠СDB=105°

Поэтому высоты из точек С и В пересекаются с продолжением сторон

Отмечаем углы и получаем ответ 30°;60° и 90°

3.

Применяем формулу

S(Δ)=(1/2)·a·b·sinα

S(Δ ABC)=(1/2)·AB·AC·sinα

S(ΔAMK)=(1/2)·AM·AK·sinα

По условию AM=(2/3)AB и S(Δ ABC)=2S(Δ AМК)

AB·AC=2·AM·AK

AB·AC=2·(2/3)AB·AK

AC=(4/3)AK

АК:АС=3:4

О т в е т. 3:4

---