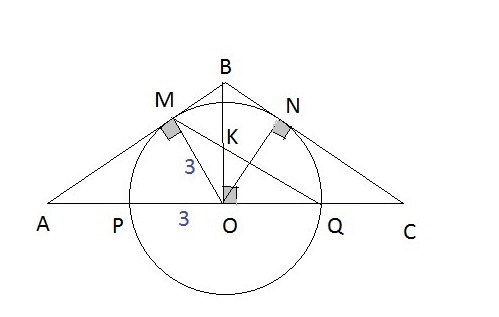
ВО- высота и одновременно биссектриса равнобедренного треугольника АВС.
ВО - биссектриса и в треугольнике ВМС.
В треугольнике ВМС - биссектриса МС делит противоположную сторону МС на отрезки, пропорциональные прилежащим сторонам треугольника.
Так как по условию
СК:КМ=7:6, то
ВС:ВМ=7:6
Пусть ВМ=х, тогда ВС=7х/6
АВ=ВС=7х/6
АМ=АВ-ВМ=(7х/6)-х=(1/6)х
В прямоугольном треугольнике АВО высота МО есть среднее пропорциональное отрезков AM и МВ.
(1/6)x*x=9
x^2=54
x=3√6
АВ=(7/6)·(3√6)=(21√6)/6
S (Δ ABC)=2S(Δ ABO)=2*(1/2)AB*MO=((21√6)/6)·3=63√6/6=21√6/2
О т в е т. 21√6/2