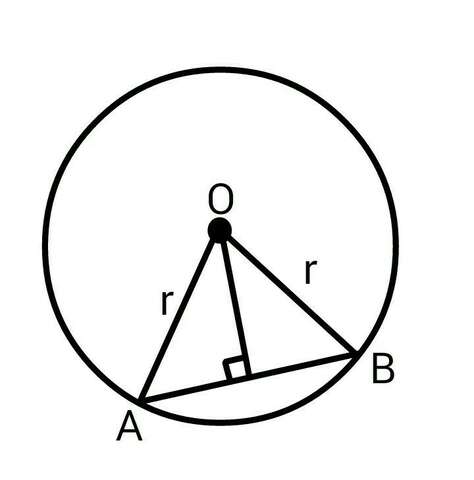
"Расстоянием" называют перпендикуляр. Поэтому нам нужно найти длину перпендикуляра из точки O на хорду AB.
Так как AO и OB радиусы, следовательно треугольник AOB равнобедренный. И перпендикуляр опущенный из точки О является и бисектрисой и высотой. Угол между AO и перпендикуляром равен 120°/2 = 60°. Угол OAB равен 180° - 90° - 60° = 30°.
Так как перпендикуляр лежит напротив угла в 30°, значит он в два раза меньше гипотенузы AO. А значит равен AO/2 = r/2.
Итак, ответ: расстояние от центра О окружности радиусом r до хорды AB равно r/2