7) 
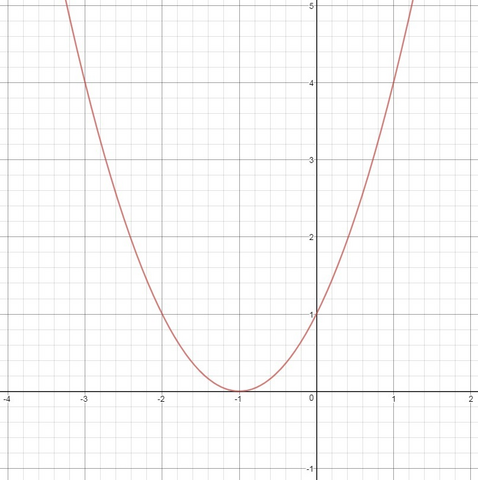
Находим вершину параболы: 
При x=-1: y=0
Эта парабола имеет 1 корень, значит касается оси Ox. Найдём ещё 2 вспомогательные точки:

Проводим параболу через три точки (вершина и корни, см. рис.)
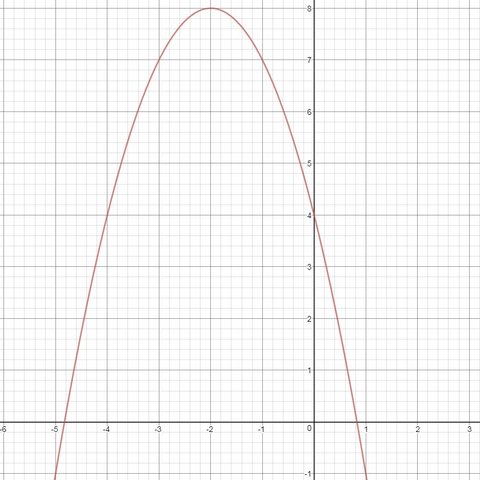
8) 
Вершина параболы: 

Ещё 2 вспомогательных точки:

Делаем аналогично следующие 2 задания
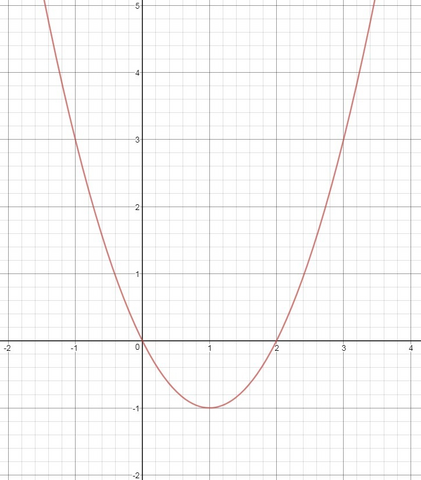
9) 
Вершина: 
Доп. точки: 
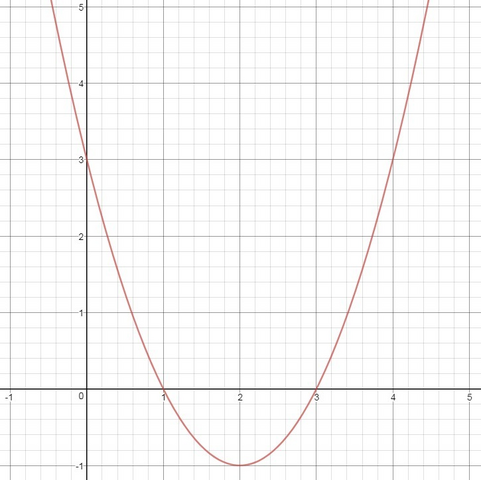
10) 
Вершина: 
Доп. точки: 
рисунки от 7 номера до 10 идут по порядку