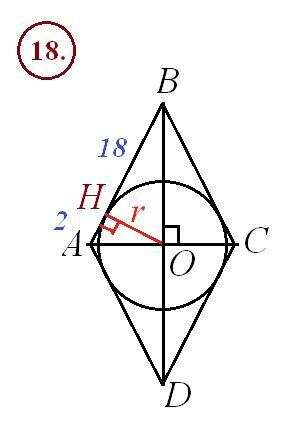18. Рассмотрим ромб АВСД (рисунок во вложении). Пусть АС и ВД - диагонали, О - точка их пересечения. Тогда О-центр вписанной окружности. Пусть Н - точка касания окружности и стороны ромба. Тогда ОН = r - радиус. По свойству ромба АС⊥ВД ⇒ ΔАОВ - прямоугольный. По свойству касательной к окружности ОН⊥АВ ⇒ ОН - высота ΔАОВ. По свойству высоты прямоугольного треугольника, проведенной к гипотенузе ОН²=АН·ВН, отсюда 
Ответ: 6.