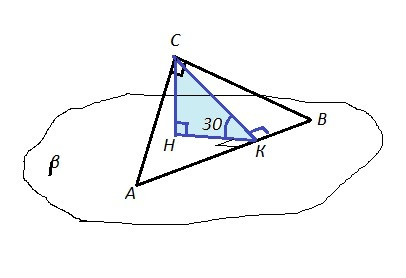
ΔАВС , ∠С=90° , С=24 см , ВС=7 см .
Найдём высоту СК, опущенную из прямого угла на гипотенузу А.
Она равна h=ab/c , где а и b - катеты, с - гипотенуза.
с=АВ=√(АС²+ВС²)=√(24²+7²)=25
h=СК=(АС·ВС)/АВ=(24·7)/25=6,72
Проведём СН⊥пл.β , соединим точку К с точкой Н. Получим ΔСКН.
∠СНК=90°, т.к. СН⊥ пл.β, а значит любой прямой, лежащей в этой пллоскости, в том числе и прямой КН.
∠СКН=30°, т.к. угол между плоскостями β и АВС равен углу между перпендикулярами в этих плоскостях, проведёнными из точки К, лежащей на линии пересечения АВ этих плоскостей: СК⊥АВ как высота ΔАВС, проведённая из т.С, КН⊥АВ по теореме о трёх перпендикулярах (СК - наклонная, СН⊥КН, СН - проекция наклонной).
Катет СН лежит против угла в 30°, поэтому он равен половине гипотенузы: СН=6,72:2=3,36 .
Ответ: длина перпендикуляра СН=3,36 см.