Высота прямоугольного треугольника, проведенная к гипотенузе, равна 12 см. может ли...

Question

Дано ответов: 2

Правильный ответ

Если провести в прямоугольном треугольнике АВС, где угол В равен 90°, высоту ВН, то эта высота делит гипотенузу на отрезки АН и НС :

Высота прямоугольного треугольника есть среднее пропорциональное для отрезков, на которые делится гипотенуза высотой.

ВН² = АН × НС

Пусть АН = х , тогда НС = 20 - х =>

12² = х × ( 20 - х )

144 = 20х - х²

х² - 20х + 144 = 0

D = ( - 20 )² - 4 × 1 × 144 = 400 - 576 = - 176 , D < 0

Корней нет

Значит, гипотенуза прямоугольного треугольника не может быть равна 20 см при высоте 12 см

ОТВЕТ: не может.

Misha001192_zn (14.8k баллов) 11 Сен, 18

NNNLLL54_zn · Answer 1 · 2018-09-10T23:11:41+0000

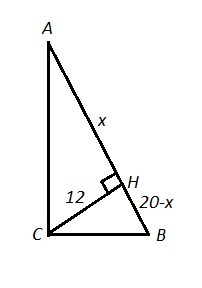
Если высота СН прямоуг. ΔАВС равна 12 см ,то гипотенуза АВ не может равняться 20 см.

По свойству высоты, проведённой из прямого угла прямоуг. треуг-ка на гипотенузу, она есть среднее пропорциональное (среднее геометрическое) между проекциями катетов на гипотенузу, то есть CH²=AH·BH .

Если гипотенуза АВ=20 см, то АВ=АН+ВН=20 см .

Обозначим АH=х , тогда ВН=(20-х) см.

$12^2=x(20-x)\\\\144=20x-x^2\\\\x^2-20x+144=0\\\\D=20^2-4\cdot 144=-176<0 \; \; \; \Rightarrow$

Уравнение не имеет действительных корней, значит не существует треугольника с гипотенузой 20 см и высотой, проведённой из вершины прямого угла , равной 12 см.