Длина окружности основания цилиндра равна 24пи см. Диагональ осевого стечения равна 26...

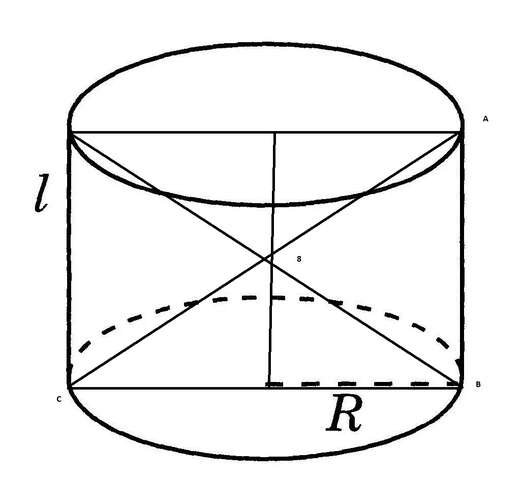
В основании цилиндра лежит окружность,формула её длины:

$c=pi*d$

$24pi=d*pi$

$d=24=CB$

Рассмотрим треугольник АВС - он прямоугольный, нам в нём известна гипотенуза и один из катетов ,совпадающий с диаметром основания. Найдём второй катет с помощью теоремы Пифагора:

$AB=\sqrt{26^2-24^2}=\sqrt{(26-24)(26+24)}=\sqrt{2*50}=10$

Найдём площадь осевого сечения.

Осевым сечением цилиндра является прямоугольник, стороны мы в нём уже нашли, одна из них совпадает с диаметром,а вторая с образующей.

$S=CB*BA$

$S=10*24=240 cm^2$