(6)
ctg(x/2) sin x≥2π
Так как
ctg(x/2)=cos(x/2)/sin(x/2) и
sin x=2sin(x/2)cos(x/2), то
(cos(x/2)/sin (x/2)) (2sin(x/2) cos(x/2))≥2π
Тк sin(x/2)≠0, то
2cos²(x/2)≥2π
cos²(x/2)-π≥0
|cos (x/2)|≤1 из свойств косинуса
поэтому cos²(x/2)≤1
а число π~3,14
(cos²(x/2)-π)≤1-3,14...<0<br>следовательно, наше неравенство не имеет решений.
(7)
sinx-5x+3≤0
sinx ≤ 5x-3
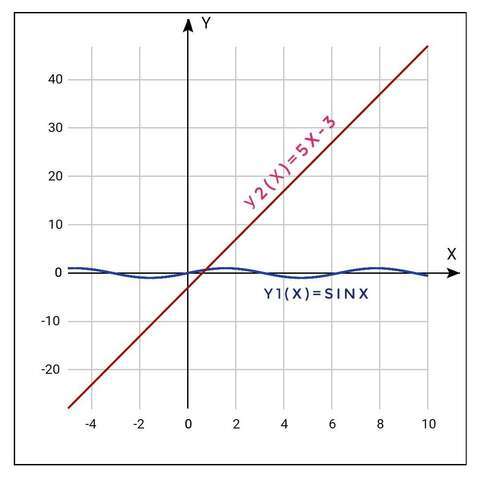
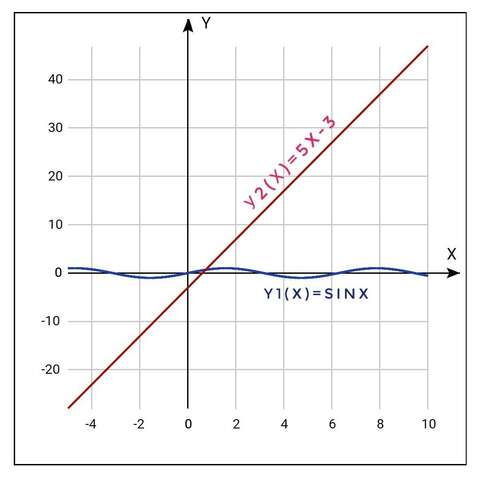
построим графики
y1(x)=sinx
y2(x)=5x-3
(см фото)
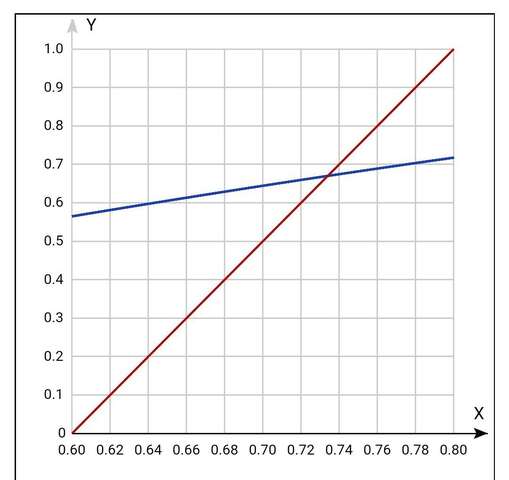
и посмотрим, где
y1(x)≤y2(x)
это случится при
x≥0,73 (приблизительно)
(8)
Определим область определения нашего неравенства:
Во-первых, из определения tgx: cosx≠0,
или x≠π/2 + πn, n€Z
во-вторых
tgx≥0 ( под квадратным корнем всегда находится неотрицательное выражение)
откуда πn ≤ x < π/2 + πn, n€Z (#)
(π/2 + πn исключили (см выше))
Затем, тк
cos²a+sin²a=1 при любых а
и следовательно , наше неравенство примет вид: 1>2-x или x>1
Объединяя полученное решение и область определения (#), получаем
πn ≤ x < π/2 + πn, n€Z ,n≥1
и 1<х<π/2<hr>